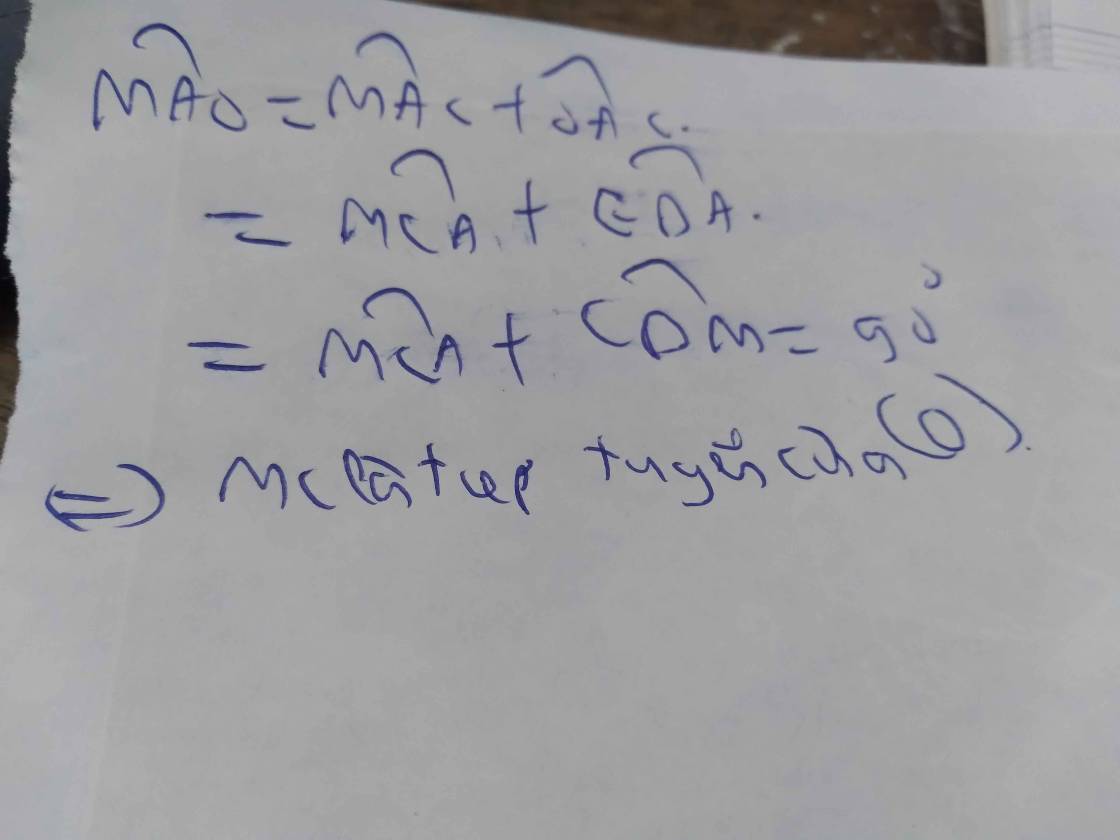bạn có thể tham khảo qua link này
https://hoidap247.com/cau-hoi/102853
Cho tam giác ABC, đường tròn tâm I nội tiếp tam giác tiếp xúc với các cạnh AB, AC, BC lần lượt tại D, E và F. DE cắt BC tại P. IF cắt đường tròn đường kính BC tại K.
CMR : PK là tiếp tuyến của đường tròn đường kính BC
1. cho tam giác ABC.Tia Ax nằm khác phía với AC đối với đường thẳng AB thỏa mãn góc xAB bằng góc ACB.chứng minh Ax là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC
2.cho nửa đường tròn (O) đường kính AB trên đoạn AB lấy điểm M,gọi H là trung điểm của AM.đường thẳng qua H vuông góc với AB cắt (O) tại C .đường tròn đường kính MB cắt BC tại I. CM HI là tiếp tuyến của đường tròn đường kính MB
3.cho nửa đường tròn tâm O đường kính AB, C thuộc nửa đường tròn.vẽ CH vuông góc với AB(H thuộc AB),M là trung điểm CH,BM cắt tiếp tuyến Ax của O tại P .chứng minh PC là tiếp tuyến của (O)
4.cho đường tròn O đường kính AB, M là một điểm trên OB.đường thẳng qua M vuông góc với AB tại M cắt O tại C và D. AC cắt BD tại P,AD cắt BC tại Q,AB cắt PQ tai I chứng minh IC,ID là tiếp tuyến của (O)
5.cho tam giác ABC nội tiếp đường tròn đường kính BC (AB<AC).T là một điểm thuộc OC.đường thẳng qua T vuông góc với BC cắt AC tại H và cắt tiếp tuyến tại A của O tại P.BH cắt (O) tại D. chứng minh PD là tiếp tuyến của O
6.cho tam giác ABC nội tiếp đường tròn O. phân giác góc BAC cắt BC tại D và cắt (O) tại M chứng minh BM là tiếp tuyến của đường tròn ngoại tiếp tam giác ABD
Cho tam giác ABC điểm D thuộc cạnh BC . Gọi M,E,N theo thứ tự là trung điểm AB, AD, AC. Đường vuông góc AB tại M và đường vuông góc AC tại N cắt nhau tại O. Đường vuông góc AD tại E cắt OM,ON tại I,K.
a, Các điểm O,I,K theo thứ tự là tâm đường tròn ngoại tiếp của tam giác nào?
b, CMR A,I,O,K thuộc cùng 1 đường tròn
Cho tam giác ABC vuông tại A, AB = 24, AC = 32. Đường trung trực của BC cắt AC, BC theo thứ tự tại D và E. Tính DE
Cho tam giác ABC vuông tại A, AB=24cm, AC=32cm. Đường trung trực của BC cắt AC, BC theo thứ tự D và E. Tính DE.
Cho tam giác ABC vuông tại A (AB<AC). Đường tròn (O) đường kính AC cắt BC tại H
a. Chứng minh AH ⊥ BC
b. Gọi M là trung điểm của Ab. Chứng minh HM là tiếp tuyến của(O)
c. Tia phân giác của góc HAC cắt BC tại E và cắt (O) tại D. Chứng minh DA.DE=DC2
d. Trường hợp AB=12cm, AC=16cm. Tính bán kính đường tròn nội tiếp ΔAMN
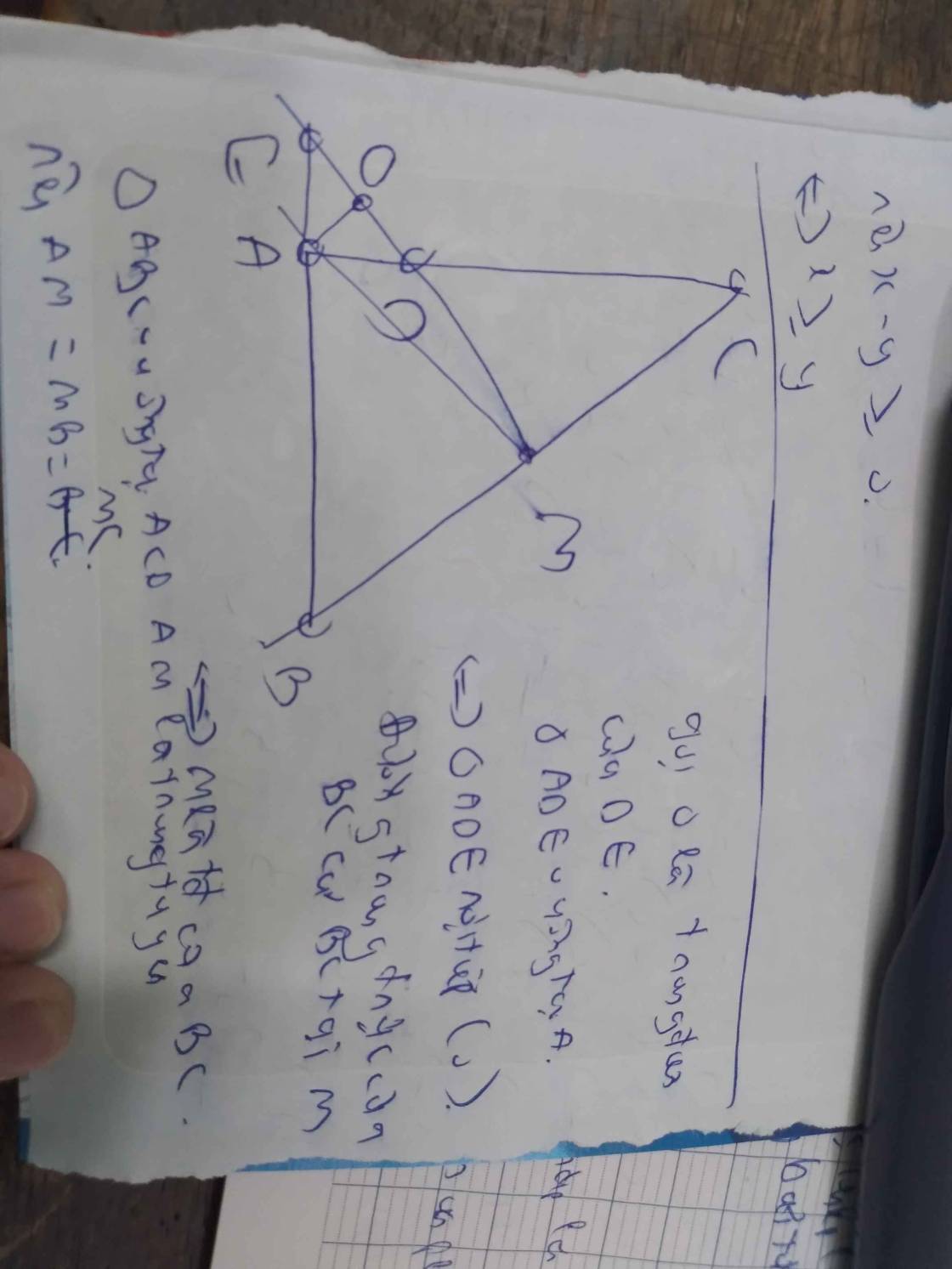
Cho tam giác ABC (AB nhỏ hơn AC) có 3 góc nhọn ,đường tròn tâm O đường kính BC cắt AB, AC lần lượt tại D và E. Gọi H là giao điểm của BE và CD, tia AH cắt cạnh BC tại F. Gọi I là trung điểm AH . Qua I kẻ đường thẳng vuông góc với AO cắt đường thẳng DE tại M. CM: AM là tiếp tuyến của đường tròn ngoại tiếp tam giác ADE
cho tam giác ABC vuông tại A (AB<AC). M là trung điểm AC. Đường tròn đường kính MC cắt BC tại N. BM kéo dài cắt đường tròn tại D
a)CM: A,B,C,D cùng thuộc 1 đường tròn
b) Gọi O là trung điểm BC, CM: OM là tiếp tuyến của đường kính MC
Cho tam giác ABC vuông tại A , đường cao AH.Vẽ đường tròn tâm O đường kính AH. Đường tròn này cắt các cạnh AB, Ác theo thứ tự ở D và E.
a) CMR: D, O , E thẳng hàng .
B) các tiếp tuyến của đường tròn tâm Ở kẻ từ D và E cắt BC lần lượt tại M,N.CMR: M và N là trung điểm của HB và HC
