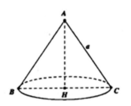
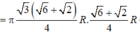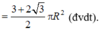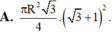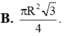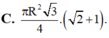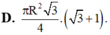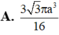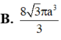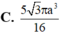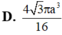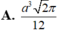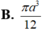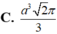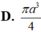Cho tam giác ABC nội tiếp trong đường tròn tâm O, bán kính R có B A C ^ = 75 0 , A C B ^ = 60 0 . Kẻ BH ⊥ AC. Quay quanh AC thì ∆ BHC tạo thành hình nón tròn xoay (N). Tính diện tích xung quanh của hình nón xoay (N) theo R.
A. 3 + 2 2 2 πR 2
B. 3 + 2 3 2 πR 2
C. 3 ( 1 + 2 ) 4 πR 2
D. 3 ( 1 + 3 ) 4 πR 2
Đáp án B
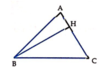
Áp dụng định lý hàm số sin, ta có
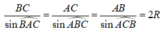
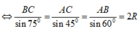
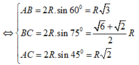
Lai có:
![]()
![]()
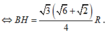
Khi quay ∆ ABC quanh AC thì ∆ BHC tạo thành hình nón tròn xoay (N) có đường sinh
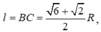
bán kính đáy
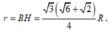
Diện tích xung quanh hình nón (N) là:
![]()