Các câu hỏi tương tự
Từ miếng bìa hình tròn kính R 4 người ta cắt một hình quạt có bán kính với hình tròn và góc
α
270
0
Sau đó xếp hình quạt thành mặt xung quanh của hình nón. Tính thể tích cùa khối nón. A.
4
π
B.
3
π
7
C.
9
π
7
D.
64...
Đọc tiếp
Từ miếng bìa hình tròn kính R= 4 người ta cắt một hình quạt có bán kính với hình tròn và góc α = 270 0 Sau đó xếp hình quạt thành mặt xung quanh của hình nón. Tính thể tích cùa khối nón.
A. 4 π
B. 3 π 7
C. 9 π 7
D. 64 π 3
Cho hình tròn tâm S, bán kính R 2. Cắt đi
1
4
hình tròn rồi dán lại để tạo ra mặt xung quanh của hình nón. Tính diện tích toàn phần của hình nón đó.
Đọc tiếp
Cho hình tròn tâm S, bán kính R = 2. Cắt đi 1 4 hình tròn rồi dán lại để tạo ra mặt xung quanh của hình nón. Tính diện tích toàn phần của hình nón đó.
![]()
![]()
![]()
![]()
Một hình nón có góc ở đỉnh bằng a, bán kính đường tròn đáy bằng a, diện tích xung quanh của hình nón bằng
Đọc tiếp
Một hình nón có góc ở đỉnh bằng a, bán kính đường tròn đáy bằng a, diện tích xung quanh của hình nón bằng
![]()
![]()
![]()
![]()
Cho tam giác ABC nội tiếp trong đường tròn tâm O, bán kính R có
B
A
C
^
75
0
,
A
C
B
^
60
0
. Kẻ BH
⊥
AC. Quay quanh AC thì
∆
BHC tạo...
Đọc tiếp
Cho tam giác ABC nội tiếp trong đường tròn tâm O, bán kính R có B A C ^ = 75 0 , A C B ^ = 60 0 . Kẻ BH ⊥ AC. Quay quanh AC thì ∆ BHC tạo thành hình nón tròn xoay (N). Tính diện tích xung quanh của hình nón xoay (N) theo R.
A. 3 + 2 2 2 πR 2
B. 3 + 2 3 2 πR 2
C. 3 ( 1 + 2 ) 4 πR 2
D. 3 ( 1 + 3 ) 4 πR 2
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng
60
0
. Tính tỉ số thể tích của hình trụ (T) và hình nón (T) .
A
.
V
T
V
N
2...
Đọc tiếp
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng 60 0 . Tính tỉ số thể tích của hình trụ (T) và hình nón (T) .
A . V T V N = 2 6
B . V T V N = 2 3
C . V T V N = 3 2
D. Đáp án khác
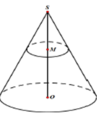
Một hình nón có chiều cao SO50cm và có bán kính đáy bằng 10cm Lấy điểm M thuộc đoạn SO sao cho OM20cm Một mặt phẳng qua M vuông góc với SO cắt hình nón theo giao tuyến là đường tròn (C). Tính diện tích xung quanh của hình nón đỉnh S có đáy là hình tròn xác định bởi (C) (xem hình vẽ).
Đọc tiếp
Một hình nón có chiều cao SO=50cm và có bán kính đáy bằng 10cm Lấy điểm M thuộc đoạn SO sao cho OM=20cm Một mặt phẳng qua M vuông góc với SO cắt hình nón theo giao tuyến là đường tròn (C). Tính diện tích xung quanh của hình nón đỉnh S có đáy là hình tròn xác định bởi (C) (xem hình vẽ).
![]()
![]()
![]()
![]()
Cho hình nón đỉnh S, đáy là đường tròn (0; 5). Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm A và B sao cho SA AB 8. Tính khoảng cách từ O đến (SAB).
Đọc tiếp
Cho hình nón đỉnh S, đáy là đường tròn (0; 5). Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm A và B sao cho SA = AB = 8. Tính khoảng cách từ O đến (SAB).
![]()
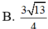
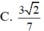
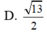
Một hình trụ có bán kính đáy bằng r và khoảng cách giữa hai đáy bằng
r
3
Một hình nón có đỉnh là tâm mặt đáy này và đáy trùng với mặt đáy kia của hình trụ. Tính tỉ số diện tích xung quanh của hình trụ và hình nón. D. 3
Đọc tiếp
Một hình trụ có bán kính đáy bằng r và khoảng cách giữa hai đáy bằng r 3 Một hình nón có đỉnh là tâm mặt đáy này và đáy trùng với mặt đáy kia của hình trụ. Tính tỉ số diện tích xung quanh của hình trụ và hình nón.
![]()
![]()
D. 3
Cho hình nón xoay đĩnh S có đáy là hình tròn (O,R) .
1. giả sử góc phẳng ở đĩnh S là 60 độ. AB là đường kính cố định của đáy.
a. C, D là hai điểm thuộc đường tròn đáy và ở về cùng một phía với đường kính AB sao cho ^ BAC phi 45 độ và ^BAD 45 độ. Tính góc nhị diện hợp bởi (SAB) và (SCD) theo Phi .
b . E,F là dây cung thay đổi của đường tròn đáy vuông góc với AB.
Tìm quỹ tích tâm vòng tròn ngoại tiếp tam giác SEF
2. Trên đáy có A là điểm cố định còn D là điểm di động.
a . Biết góc...
Đọc tiếp
Cho hình nón xoay đĩnh S có đáy là hình tròn (O,R) .
1. giả sử góc phẳng ở đĩnh S là 60 độ. AB là đường kính cố định của đáy.
a. C, D là hai điểm thuộc đường tròn đáy và ở về cùng một phía với đường kính AB sao cho ^ BAC = phi < 45 độ và ^BAD = 45 độ. Tính góc nhị diện hợp bởi (SAB) và (SCD) theo Phi .
b . E,F là dây cung thay đổi của đường tròn đáy vuông góc với AB.
Tìm quỹ tích tâm vòng tròn ngoại tiếp tam giác SEF
2. Trên đáy có A là điểm cố định còn D là điểm di động.
a . Biết góc AOD = alpha , nhị diện cạnh AD = Bêta và khoảng cách từ O đến mp ( SAD) bằng a . Tính thể tích hình nón theo a, alpha, bêta.
b. Xác định D để tam giác SAD có diện tích lớn nhất.
c . Tìm quỷ tích hình chiếu vuông góc H của O lên mp (SAD) khi D thay đổi.





