
+ R, P lần lượt là điểm chính giữa các cung 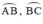
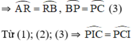
⇒ ΔPCI cân tại P.


+ R, P lần lượt là điểm chính giữa các cung 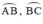
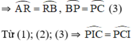
⇒ ΔPCI cân tại P.
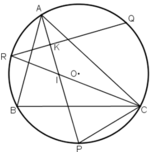
Cho tam giác ABC nội tiếp đường tròn. P,Q,R theo thứ tự là các điểm chính giữa của các cung bị chắn BC, CA, AB bởi các góc A, B, C.
a) Chứng minh AP ⊥ QR.
b) AP cắt CR tại I. Chứng minh tam giác CPI là tam giác cân.
Cho tam giác ABC nội tiếp đường tròn. P,Q,R theo thứ tự là các điểm chính giữa các cung bị chắn BC,CA,AB bởi các góc A,B,C. Có: AP⊥QR. Vẽ AP cắt CR tại I, ta được tam giác CPI là tam giác cân. Cho điểm A di chuyển trên cung lớn BC, hỏi I di chuyển trên đường nào?
Cho tam giác ABC nội tiếp đường tròn. P,Q,R theo thứ tự là các điểm chính giữa của các cung bị chắn BC, CA, AB bởi các góc A, B, C.
Chứng minh AP ⊥ QR.
Cho ∆ABC nội tiếp đường tròn (O) . Gọi P;Q;R lần lượt là điểm chính giữa của các cung BC, CA, AB
a) chứng minh AP ⊥QR
b) AP cắt CR tại I. Chứng minh ∆CPI cân
Cho tam giác nhọn ABC. Trên nửa mặt phẳng bờ AC không chứa điểm B, lấy điểm D sao cho DA = DC, \(\widehat{ACD}=\frac{1}{2}\widehat{ABC}\)
a. CM tg ABCD nội tiếp
b. Trên đường tròn ngoại tiếp tg ABCD, lấy E,F theo thứ tự là các điểm chính giữa của các cung bị chắn CB, BA bởi các góc CAB, góc BCA. Chứng minh BD vuông góc EF.
c. Gọi M là giao điểm BD và CF. CMR tam giác CDM cân.
cho tam giác nhọn ABC nội tiếp đường tròn tâm O. M là điểm chính giữa cung BC không chứa điểm A. Gọi M' là điểm đối xứng với M qua O. Các đường phân giác trong góc B và góc C của tam giác ABC cắt đường thẳng AM' lần lượt tại E và F.
1/Chứng minh tứ giác BCEF nội tiếp được trong đường tròn
2/Biết đường tròn nội tiếp tam giác ABC có tâm I bán Kính r.
Chứng Minh: IB.IC = 2r.IM
cho tam giác ABC , 3 góc nhọn nội tiếp đường tròn (O). M, N, K lần lượt là các điểm chính giữa của các cung BC, AC , AB
a) AM vuông góc NK
b) AM giao CK tại I . Chứng minh tam giác CIM cân
Bài 3: Cho tam giác ABC. Gọi (P), (Q), (R) theo thứ tự là các đường tròn bàng tiếp trong các góc A, B, C. Gọi tiếp điểm của (Q), (R) trên đường thẳng BC theo thứ tự E, F. Chứng minh rằng CE = BF. Gọi H, I, K theo thứ tự là tiếp điểm của các đường tròn (P), (Q), (R) với các cạnh BC, AC, AB. Nếu AH = BI = CK thì tam giác ABC là tam giác gì?
1) cho tam giác vuông ABC đường cao AH .gọi AD ;AE là phân giác các góc BAH và góc CAH .chứng minh rằng đường tròn nội tiếp tam giác BCA trùng với đường tròn ngoại tiếp tam giác ADE
2)cho tam giác ABC vuông tại A;gọi I là tâm đường tròn nội tiếp tam giác ABC ;các tiếp điểm trên BC;CA;AB lần lượt là D,E,F.gọi M là trung điểm của AC ,đường thẳng MI cắt các cạnh AB tại N ,đường thẳng DF cắt đường cao AH tại P .cmr tam giác APN cân