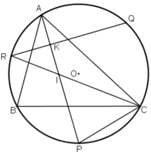
Gọi K là giao điểm của QR và AP.
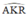 là góc có đỉnh K nằm bên trong đường tròn
là góc có đỉnh K nằm bên trong đường tròn
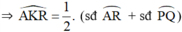

⇒ AP ⊥ QR.

Gọi K là giao điểm của QR và AP.
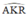 là góc có đỉnh K nằm bên trong đường tròn
là góc có đỉnh K nằm bên trong đường tròn
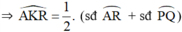

⇒ AP ⊥ QR.
Cho tam giác ABC nội tiếp đường tròn. P,Q,R theo thứ tự là các điểm chính giữa của các cung bị chắn BC, CA, AB bởi các góc A, B, C.
a) Chứng minh AP ⊥ QR.
b) AP cắt CR tại I. Chứng minh tam giác CPI là tam giác cân.
Cho tam giác ABC nội tiếp đường tròn. P,Q,R theo thứ tự là các điểm chính giữa của các cung bị chắn BC, CA, AB bởi các góc A, B, C.
AP cắt CR tại I. Chứng minh tam giác CPI là tam giác cân.
Cho tam giác ABC nội tiếp đường tròn. P,Q,R theo thứ tự là các điểm chính giữa các cung bị chắn BC,CA,AB bởi các góc A,B,C. Có: AP⊥QR. Vẽ AP cắt CR tại I, ta được tam giác CPI là tam giác cân. Cho điểm A di chuyển trên cung lớn BC, hỏi I di chuyển trên đường nào?
Cho tam giác nhọn ABC. Trên nửa mặt phẳng bờ AC không chứa điểm B, lấy điểm D sao cho DA = DC, \(\widehat{ACD}=\frac{1}{2}\widehat{ABC}\)
a. CM tg ABCD nội tiếp
b. Trên đường tròn ngoại tiếp tg ABCD, lấy E,F theo thứ tự là các điểm chính giữa của các cung bị chắn CB, BA bởi các góc CAB, góc BCA. Chứng minh BD vuông góc EF.
c. Gọi M là giao điểm BD và CF. CMR tam giác CDM cân.
Bài 3: Cho tam giác ABC. Gọi (P), (Q), (R) theo thứ tự là các đường tròn bàng tiếp trong các góc A, B, C. Gọi tiếp điểm của (Q), (R) trên đường thẳng BC theo thứ tự E, F. Chứng minh rằng CE = BF. Gọi H, I, K theo thứ tự là tiếp điểm của các đường tròn (P), (Q), (R) với các cạnh BC, AC, AB. Nếu AH = BI = CK thì tam giác ABC là tam giác gì?
Cho ∆ABC nội tiếp đường tròn (O) . Gọi P;Q;R lần lượt là điểm chính giữa của các cung BC, CA, AB
a) chứng minh AP ⊥QR
b) AP cắt CR tại I. Chứng minh ∆CPI cân
Các thầy cô, các bạn giúp em với!!! Em cảm ơn trước!
Cho tam giác vuông ABC (BC > AB, góc B=90 độ). Gọi I là tâm đường tròn nội tiếp tam giác ABC, các tiếp điểm của đường tròn nội tiếp với cạnh AB, BC, CA lần lượt là P, Q, R.
1) Chứng minh tứ giác BPIQ là hình vuông. (bỏ qua )
2) Đường thẳng BI cắt QR tại D. Chứng minh 5 điểm P, A, R, D, I nằm trên một đường tròn.
3) Đường thẳng AI và CI kéo dài cắt BC, AB lần lượt tại E và F. Chứng minh AE. CF = 2AI. CI.
Cho tam giác ABC có BAC > 90°, đường tròn tâm I nội tiếp tam giác ABC và tiếp xúc với các cạnh AB, BC và CA lần lượt tại P, Q và R. Gọi M, N theo thứ tự là trung điểm của các cạnh CA, AB. Các đường thẳng MN, PQ cắt nhau ở D. a) Cho biết độ dài các cạnh AB, BC và CA của tam giác tương ứng bằng 4 cm, 7 cm và 5 cm, tính độ dài của đoạn AP theo cm. (Đã tính AP=1cm) b) Chứng minh các tam giác NDP và MCD là các tam giác cân. c) Chứng minh rằng các điểm D, I, C thẳng hàng. d) Gọi H là chân đường vuông góc kẻ từ Q đến PR. Chứng minh PHB = CHR
Cho tam giác ABC không đều, BC là cạnh ngắn nhất. Đường tròn nội tiếp (I) của tam giác ABC theo thứ tự tiếp xúc với BC, CA, AB tại X, Y, Z. Gọi G là trọng tâm tam giác XYZ. Trên các tia BA, CA theo thứ tự lấy các điểm E, F sao cho BE = CF = BC. Chứng minh IG vuông góc với EF.