Ta có: M I C ^ = C H M ^ = 90 0
=> MIHC nội tiếp (hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc vuông)

Ta có: M I C ^ = C H M ^ = 90 0
=> MIHC nội tiếp (hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc vuông)
Cho tam giác ABC nhọn nội tiếp đường tròn (O). M là điểm thuộc đường tròn. Vẽ MH vuông góc với BC tại H, vễ MI vuông góc với AC. Chứng minh MIHC là tứ giác nội tiếp
cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (0). M là điểm thuộc cung nhỏ AC. vẽ MH vuông góc với BC, vẽ MI vuông AC tại I, chứng minh:
1. IHM=ICM
2.đường thẳng HI cắt đường thẳng AB tại K,. chứng minh: MK vuông BK
3. DF cắt EB tại M, HF cắt EC tại N. chứng minh tam giác MIH đồng dạng với MAB
4, gọi E là trung điểm IH và F là trung điểm AB. chứng minh tứ giác KMEF nội tiếp, suy ra ME vuông góc với EF
cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O , trên cung nhỏ BC lấy điểm M sao cho MB lớn hơn MC.Kẻ MI vuông góc với AB tại I , MH vuông góc với BC tại H
a,chứng minh tứ giác BIHM nội tiếp
b,gọi K là giao điểm của IH và AC . chứng minh : góc MIK bằng góc MAK và MK vuông góc với AC
c,tìm vị trí của M trên cung nhỏ BC để IK đạt giá trị lớn nhất
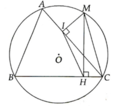
Cho tam giác ABC có ba góc nhọn nội tiếp (O), M là điểm thuộc cung nhỏ AC. Vẽ MH vuông góc với BC tại H, MI vuông góc AC tại I
a, Chứng minh I H M ^ = I C M ^
b, Đường thẳng HI cắt đường thẳng AB tại K. Chứng minh MK vuông góc vói BK
c, Chứng minh tam giác MIH đồng dạng vói tam giác MAB
d, Gọi E là trung điểm của IH và F là trung điểm AB. Chứng minh tứ giác KMEF nội tiếp từ đó suy ra ME vuông góc vói EF
Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O). Tiếp tuyến tại A của đường tròn (O) cắt đường thẳng BC tại D. Vẽ OM vuông góc với BC tại M. a) Chứng minh tứ giác AOMD nội tiếp. b) Tia OM cắt đường tròn (O) tại điểm N, AN và BC cắt nhau tại I. Chứng minh AN là tia phân giác của góc BAC và AD=DI c) Tia phân giác của ABC cắt AN tại H. Giả sử dây AB cố định và điểm C di chuyển trên đường tròn (O) sao cho tam giác ABC nhọn (AB
Cho tam giác ABC nhọn ( AB<AC) nội tiếp đường tròn O vẽ đường kính AD . Đường thẳng B vuông góc với AC tại E cắt AC tại F. Gọi H là hình chiếu vuông góc của B trên AC. M là trung điểm của BC
a) chứng minh tứ giác CDEF nội tiếp
b) chứng minh góc MHC + góc BAD = 90°
cho tam giác MAB có 3 góc nhọn nội tiếp đường tròn O. Vẽ MH vuông gócc với AB tại H, HD vuông góc với AM tại D, HC vuông góc với MB tại C.
1. chứng minh tứ giác MDHC là tứ giác nội tiếp đường tròn
2. chứng minh góc MDC = góc MHB
3. Chứng minh MO vuông góc với CD
Giúp tôi câu 3 mọi người ơi.
Bài 2: Cho tam giác ABC có các góc đều nhọn góc A = 45 độ. Vẽ các đường cao BD và CE của tam giác ABC. Gọi H là giao điển của BD và CE.
1 chứng minh tứ giác AHDE là tứ giác nội tiếp
2. chứng minh HD = DC
3. Tính tỷ số DE/BC
giúp tôi ý 3
cho tam giác ABC nhọn (AB<AC) nội tiếp đường tròn tâm O . điểm M thuộc cung nhỏ BC . vẽ MD , ME , MF lần lượt vuông góc với AB , , AC tại D,E,F
A/chứng minh các tứ giác MEFC nội tiếp và góc DBM = góc DEM
B/ chứng minh D,E,F thẳng hàng và MB.MF=MD.MC
C/gọi V là trực tâm của tam giác ABC . tia BV cắt đường tròn O tại R . chứng minh góc FRV = góc FVR . từ đó suy ra DE đi qua trung điểm của VM
thank :))