a) Xét tứ giác BFEC có:
∠(BFC) = ∠(BEC) = 90 0 (gt)
Mà 2 góc này cùng nhìn cạnh BC
⇒ Tứ giác BFEC nội tiếp được đường tròn

a) Xét tứ giác BFEC có:
∠(BFC) = ∠(BEC) = 90 0 (gt)
Mà 2 góc này cùng nhìn cạnh BC
⇒ Tứ giác BFEC nội tiếp được đường tròn
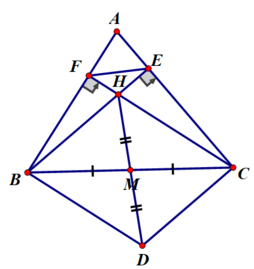
Cho tam giác ABC, hai đường cao BE và CF cắt nhau tại H. Gọi D là điểm đối xứng của H qua trung điểm M của BC
c) Chứng minh tứ giác ABDC nội tiếp được đường tròn
Cho tam giác ABC ( AB<AC) nội tiếp đường tròn (O) , bán kính R , đường cao AD,BE,CF của tam giác ABC cắt nhau tại H.
Chứng minh:
1) tứ giác BFHD,BFEC nội tiếp đường tròn
2) FH là tia phân giác của góc DFE và H là tâm đường tròn nội tiếp tam giác DEF
3) Gọi M là trung điểm BC . Chứng minh OM//AD và tứ giác DMEF nội tiếp
4) Gọi N là giao điểm AD và BF , chứng minh 1/HN - 1/HD = 2/AH
5) Gọi K là giao điểm AD và đường tròn (O) , khác A . Chứng minh HK đối xứng qua BC
Cho tam giác ABC nội tiếp (O;R) đường cao AD, BE, CF cắt nhau tại H. K là điểm đối xứng của H qua BC a) Chứng minh tứ giác ACKB nội tiếp đường tròn b) vẽ đường kính AM, I là trung điểm BC chứng minh H,I,M thẳng hàng
Cho ![]() có 3 góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H
có 3 góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H
a) Chứng minh rằng: tứ giác BFEC nội tiếp
b) Gọi I là điểm đối xứng của A qua O và M là trung điểm của BC. Chứng minh rằng BHCI là hình bình hành và AH=2OM
c) Gọi N là trung điểm của EF. Chứng minh rằng R.AN=AM.OM
Cho △ABC có ba góc nhọn nội tiếp đường tròn (O). Vẽ ba đường cao AD, BE, CF cắt nhau tại H. Gọi M là điểm đối xứng của H qua BC.
a) Chứng minh: tứ giác ABMC nội tiếpb) Gọi Q là trung điểm của AB. Chứng minh: QE là tiếp tuyến của đường tròn ngoại tiếp △EHCc) Hai tia BE và CF cắt đường tròn (O) lần lượt tại N và P. Tính giá trị biểu thức: T=AMAD+BNBE+CPCFCho tam giác ABC có hai đường cao BE, CF cắt nhau tại H. Gọi E' là điểm đối xứng H qua AC, F' là điểm đối xứng H qua AB. Chứng minh:
a, Tứ giác BCE'F' nội tiếp đường tròn (O)
b, Năm điểm A, F', B, C, E' cùng thuộc một đường tròn
c, AO và EF vuông góc nhau
d, Khi A chạy trên (O) thì bán kính đường tròn ngoại tiếp tam giác AEF không đổi
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O;R) và hai đường cao BF,CE cắt nhau tại H . Gọi D là điểm đối xứng với H qua trung điểm K của BC
1) Chứng minh: tứ giác BHCD là hình bình hành
2) Đường thẳng qua D và song song với BC cắt đường thẳng AH tại M. Chứng minh rằng: năm điểm A, B ,C , D , M cùng thuộc một đường tròn.
Cho tam giác ABC, hai đường cao BE và CF cắt nhau tại H. Gọi D là điểm đối xứng của H qua trung điểm M của BC
b) Chứng minh AB.AF = AC.AE