b) Xét ΔABF và ΔACE có:
∠(BEA) = ∠(CFA) = 90 0 (gt)
∠(BAC ) chung
⇒ ΔABF ∼ ΔACE (g.g)
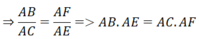

b) Xét ΔABF và ΔACE có:
∠(BEA) = ∠(CFA) = 90 0 (gt)
∠(BAC ) chung
⇒ ΔABF ∼ ΔACE (g.g)
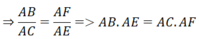
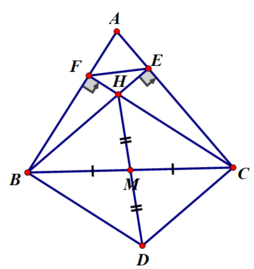
Cho tam giác ABC, hai đường cao BE và CF cắt nhau tại H. Gọi D là điểm đối xứng của H qua trung điểm M của BC
a) Chứng minh tứ giác BFEC nội tiếp được đường tròn
Cho tam giác ABC, hai đường cao BE và CF cắt nhau tại H. Gọi D là điểm đối xứng của H qua trung điểm M của BC
c) Chứng minh tứ giác ABDC nội tiếp được đường tròn
Cho ∆ABC có 3 góc nhọn AB < AC. Các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC. K là điểm đối xứng với H qua M. Chứng minh: BK ⊥ AB và CK ⊥ AC
Cho ∆ABC có 3 góc nhọn AB < AC. Các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC. K là điểm đối xứng với H qua M. Chứng minh: BK ⊥ AB và CK ⊥ AC
Cho tam giác ABC nội tiếp (O;R) đường cao AD, BE, CF cắt nhau tại H. K là điểm đối xứng của H qua BC a) Chứng minh tứ giác ACKB nội tiếp đường tròn b) vẽ đường kính AM, I là trung điểm BC chứng minh H,I,M thẳng hàng
Bài: Cho tam giác ABC (AB < AC) có hai đường cao BD và CE cắt nhau tại H. Lấy I là trung điểm của BC.
a) Chứng minh AH vuông góc với BC.
b) Gọi K là điểm đối xứng của H qua I. Chứng minh CK // BD và tam giác ABK vuông c) Chứng minh BE. BA =BH. BD d) Kẻ DM vuông góc với BC. Chứng minh MB.MC = DC^2 – MC^2
Cho △ABC có ba góc nhọn nội tiếp đường tròn (O). Vẽ ba đường cao AD, BE, CF cắt nhau tại H. Gọi M là điểm đối xứng của H qua BC.
a) Chứng minh: tứ giác ABMC nội tiếpb) Gọi Q là trung điểm của AB. Chứng minh: QE là tiếp tuyến của đường tròn ngoại tiếp △EHCc) Hai tia BE và CF cắt đường tròn (O) lần lượt tại N và P. Tính giá trị biểu thức: T=AMAD+BNBE+CPCFCho tam giác ABC có hai đường cao BE, CF cắt nhau tại H. Gọi E' là điểm đối xứng H qua AC, F' là điểm đối xứng H qua AB. Chứng minh:
a, Tứ giác BCE'F' nội tiếp đường tròn (O)
b, Năm điểm A, F', B, C, E' cùng thuộc một đường tròn
c, AO và EF vuông góc nhau
d, Khi A chạy trên (O) thì bán kính đường tròn ngoại tiếp tam giác AEF không đổi