NHỜ 500 AE GIÚP MỀNH ZS .... NGÀY MAI PHẢI NỘP OY
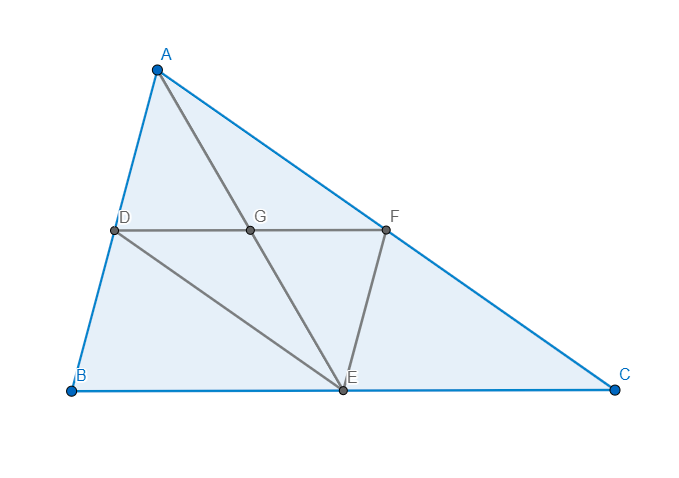
1. Cho tam giác ABC cân tại A có góc B=60 độ, đường cao AM. Trên tia đối của tia MA lấy điểm E sao cho ME=MA
a) CM: Tứ giác ABEC là hình thoi và tính số đo góc BEC
b) Hai điểm D,E đối xứng nhau qua điểm C. Đường thẳng qua E song song với BC cắt AC tại F. Tứ giác ADFE là hình gì?Vì sao?
c) CM: Tứ giác ABEF là hình thang cân
d) Điểm C có là trực tâm của tam giác DBF không ? Giải thích?
2. Cho tam giác ABC(AB<AC), đoạn AI là đường cao và ba điểm D,E,F theo thứ tự là trung điểm của các đoạn thẳng AB,AC,BC.
a) CM: Tứ giác BDEF là hình bình hànhb) Điểm J là điểm dối xứng của điểm I qua điểm E. Tứ giác AICJ là hình gì? Vì sao?
b) Điểm J là điểm đối xứng của diểm I qua điểm E. Tứ giác AICJ là hình gì? Vì sao?
c) Hai đường thẳng BE,DF cắt nhau tại K. CM : Hai tứ giác ADKE và KECF có diện tích bằng nhau
d) Tính diện tích tam giác ADE theo diện tích tam giác ABC
3. Cho tam giác ABC cân tại A, trung tuyến AM. Gọi D là điểm đối xứng của A qua M. Gọi K là trung điểm của MC, E là điểm đối xứng của D qua K.
a) CM: Tứ giác ABDC là hình thoi
b) CM: Tứ giác AMCE là hình chữ nhật
c) AM và BE cắt nhau tại I. CM : I là trung điểm của BE
d) CM: AK,CI,EM đồng quy
4. Cho hình chữ nhật ABCD(AB>AD), trên cạnh AD, BC lần lượt lấy các điểm M,N sao cho AM=CN.
a) CMR: BM song song với DN
b) Gọi O là trung điểm của BD. CMR: AC,BD,MN đồng quy tại O
c) Qua O vẽ đường thẳng d vuông góc với BD, d cắt AB tại P, cắt CD tại Q. CMR : PBQD là hinh thoi
d) Đường thẳng qua B song song với PQ và đường thẳng qua Q song song với BD cắt nhau tại K. CMR : AC vuông góc với CK.
5. Cho tam giác ABC cân tại Acó M là trung điểm của cạnh BC . Gọi D là điểm đối xứng với A qua M.
a) CM : Tứ giác ABDC là hình thoi
b) Vẽ đường thẳng vuông góc với BC tại B cắt tia CA tại điểm F. CM: Tứ giác ADBF là hình bình hành
c) Qua C vẽ đường thẳng song song với AD cắt tia BA tại điểm E. CM: Tứ giác BCEF là hình chữ nhật
d) Nối EM cắt AC tại N, kéo dài BN cắt EC tại I. CM: SIBC = 1/4 SBCEF
6. Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo . Lấy một điểm E nằm giữa hai điểm O và B. Gọi F là điểm đối xứng với điểm A qua E và I là trung điểm của CF.
a) CM: Tứ giác OEFC là hình thang và tứ giác OEIC là hình bình hành
b) Gọi H và K lần lượt là hình chiếu của điểm F trên các đường thẳng BC và CD. CM: Tứ giác CHFK là hình chữ nhật và I là trung điểm của HK
c) CM: ba điểm E,H,K thẳng hàng