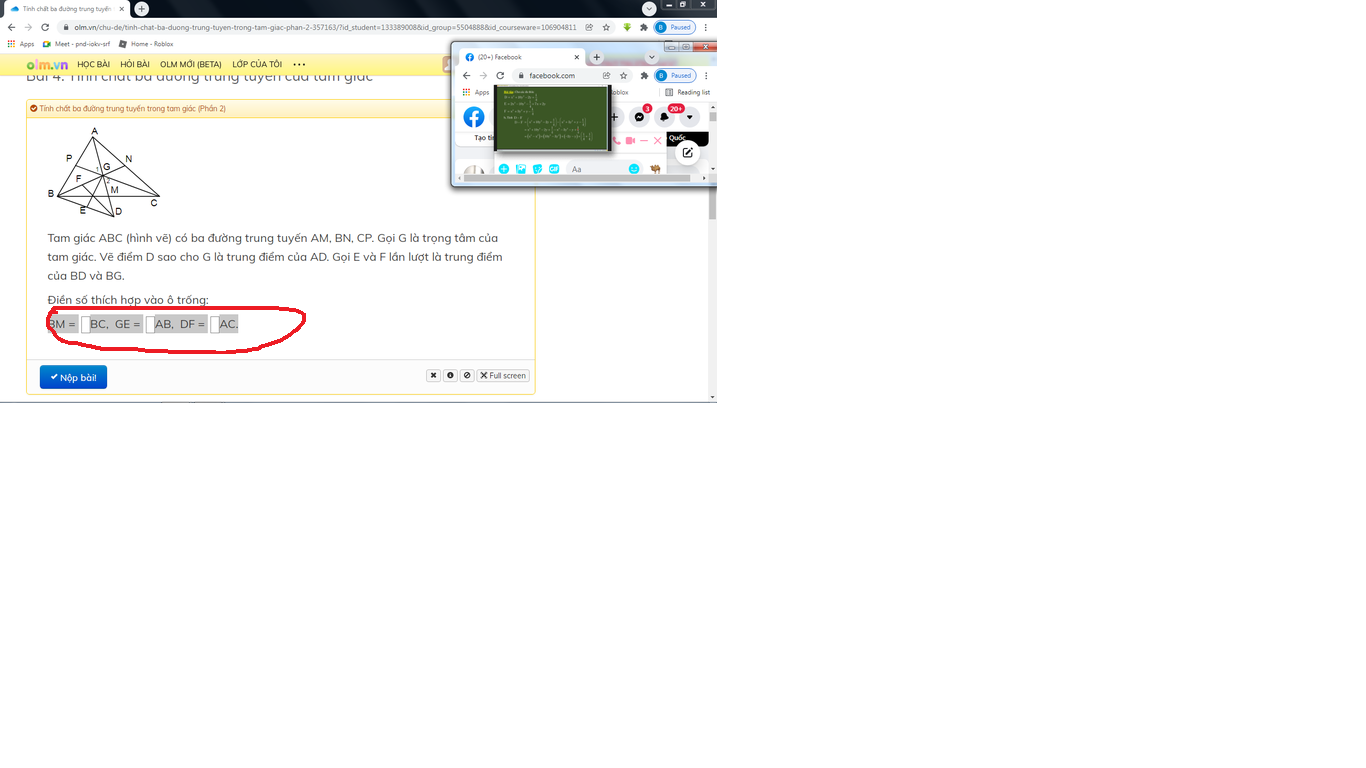
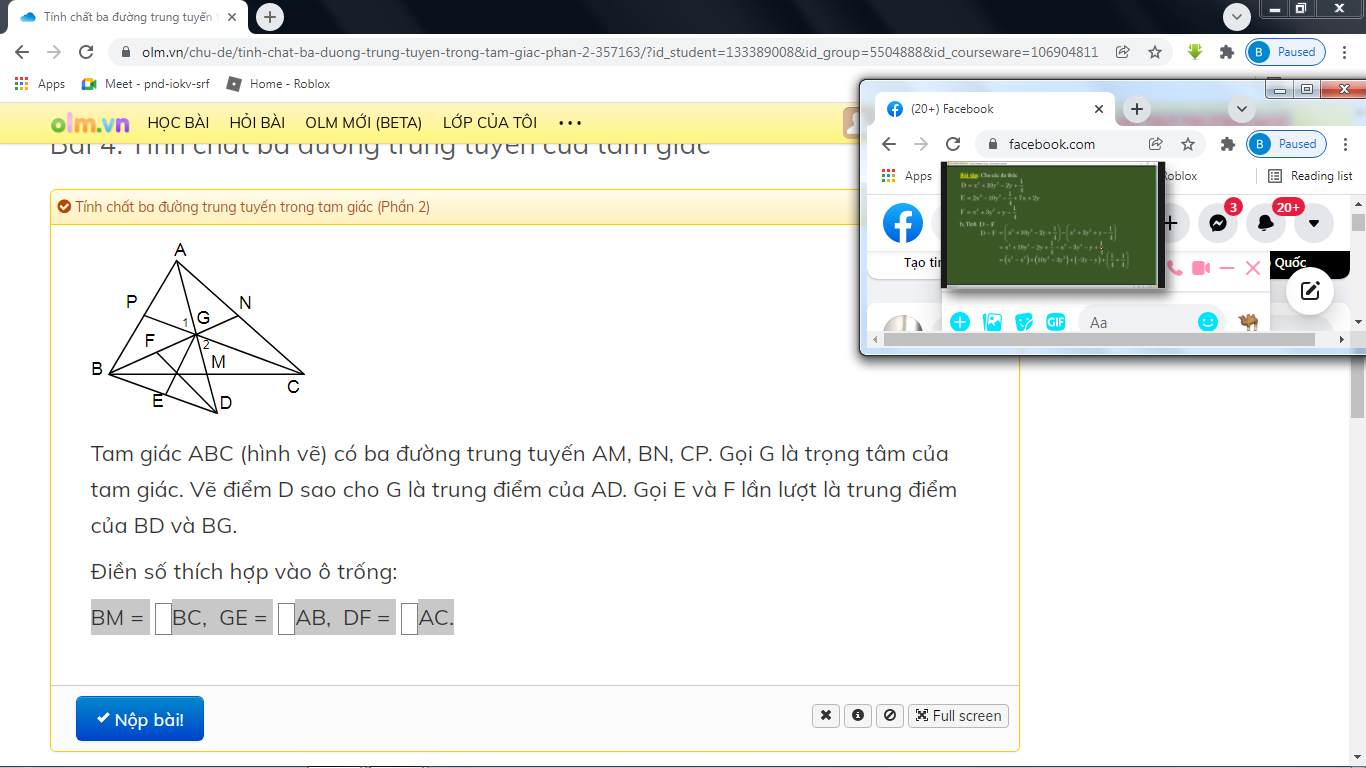
a: Xét ΔGEB và ΔGMC có
GE=GM
\(\widehat{EGB}=\widehat{MGC}\)(hai góc đối đỉnh)
GB=GC
Do đó: ΔGEB=ΔGMC
=>CM=BE
mà BE=ED=DF
nên DF=CM
b: Xét ΔDAF và ΔDCE có
DA=DC
\(\widehat{ADF}=\widehat{CDE}\)
DF=DE
Do đó: ΔDAF=ΔDCE
=>AF=CE(1)
Xét ΔGEC và ΔGMB có
GE=GM
\(\widehat{EGC}=\widehat{MGB}\)(hai góc đối đỉnh)
GC=GB
Do đó: ΔGEC=ΔGMB
=>EC=MB(2)
Từ (1) và (2) suy ra AF=BM
c: Xét ΔGEB và ΔGMC có
GE=GM
\(\widehat{EGB}=\widehat{MGC}\)(hai góc đối đỉnh)
GB=GC
Do đó: ΔGEB=ΔGMC
=>EB=MC
Xét ΔEBM và ΔMCE có
EB=MC
EM chung
BM=CE
Do đó: ΔEBM=ΔMCE
=>\(\widehat{EBM}=\widehat{MCE}\)(3)
Ta có: ΔGEC=ΔGMB
=>\(\widehat{GEC}=\widehat{GMB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên EC//BM
=>\(\widehat{DEC}=\widehat{EBM}\)(hai góc đồng vị)(4)
Ta có: ΔDEC=ΔDFA
=>\(\widehat{DEC}=\widehat{DFA}\)(5)
Từ (3),(4),(5) suy ra \(\widehat{ECM}=\widehat{AFD}\)
Xét ΔMEC và ΔDAF có
CE=FA
\(\widehat{ECM}=\widehat{AFD}\)
CM=FD
Do đó: ΔMEC=ΔDAF
d: Xét ΔBDC có
G,E lần lượt là trung điểm của BC,BD
=>GE là đường trung bình của ΔBDC
=>GE//DC và \(GE=\dfrac{DC}{2}\)