Các câu hỏi tương tự
Cho tứ diện ABCD có AD
⊥
(ABC), ABC là tam giác vuông tại B. Biết BCA, ABa
3
, AD3a Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng
Đọc tiếp
Cho tứ diện ABCD có AD ⊥ (ABC), ABC là tam giác vuông tại B. Biết
BC=A, AB=a 3 , AD=3a Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng
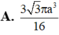
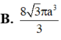
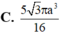
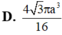
Cho tam giác ABC có AB3, BC5, CA7 Tính thể tích của khối tròn xoay sinh ra là do hình tam giác ABC quay quanh đường thẳng AB:
Đọc tiếp
Cho tam giác ABC có AB=3, BC=5, CA=7 Tính thể tích của khối tròn xoay sinh ra là do hình tam giác ABC quay quanh đường thẳng AB:
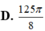
Cho tam giác ABC vuông tại B có AC2a, BCa khi quay tam giác ABC quay quanh cạnh góc vuông AB thì đường gấp khúc ABC tạo thành một hình nón tròn xoay có diện tích xung quanh bằng
Đọc tiếp
Cho tam giác ABC vuông tại B có AC=2a, BC=a khi quay tam giác ABC quay quanh cạnh góc vuông AB thì đường gấp khúc ABC tạo thành một hình nón tròn xoay có diện tích xung quanh bằng
Cho tam giác ABC có Quay tam giác ABC xung quanh cạnh BC ta đuợc khối tròn xoay có thể tích V bằng:
Đọc tiếp
Cho tam giác ABC có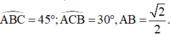 
Quay tam giác ABC xung quanh cạnh BC ta đuợc khối tròn xoay có thể tích V bằng:
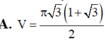
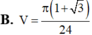
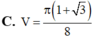
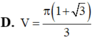
Cho tam giác OAB vuông tại O, OAOB 4. Lấy một điểm M thuộc cạnh AB và gọi H là hình chiếu của M trên OA. Thể tích của khối tròn xoay được tạo thành khi quay tam giác OMH quanh OA có thể tích lớn nhất bằng A.
256
π
81
B.
81
π
256...
Đọc tiếp
Cho tam giác OAB vuông tại O, OA=OB= 4. Lấy một điểm M thuộc cạnh AB và gọi H là hình chiếu của M trên OA. Thể tích của khối tròn xoay được tạo thành khi quay tam giác OMH quanh OA có thể tích lớn nhất bằng
A. 256 π 81
B. 81 π 256
C. 128 π 81
D. 8 π 3
Tính thể tích khối tròn xoay sinh ra khi quay tam giác đều ABC cạnh bằng 1 quanh AB A.
3
π
4
B.
π
4
C.
π
8
D.
π
3
2
Đọc tiếp
Tính thể tích khối tròn xoay sinh ra khi quay tam giác đều ABC cạnh bằng 1 quanh AB
A. 3 π 4
B. π 4
C. π 8
D. π 3 2
Cho tam giác ABC có BAC
120
o
. Quay tam giác ABC (bao gồm cả điểm trong tam giác) quanh đường thẳng AB ta được một khối tròn xoay. Thể tích khối tròn xoay đó bằng :
Đọc tiếp
Cho tam giác ABC có BAC= 120 o . Quay tam giác ABC (bao gồm cả điểm trong tam giác) quanh đường thẳng AB ta được một khối tròn xoay. Thể tích khối tròn xoay đó bằng :
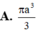
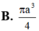
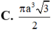
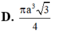
Tam giác ABC vuông cân đỉnh A có cạnh huyền là 2. Quay hình tam giác ABC quanh trục BC thì được khối tròn xoay có thể tích là: A.
2
2
3
π
B.
4
3
π
C.
2
3
π
D.
1
3
π
Đọc tiếp
Tam giác ABC vuông cân đỉnh A có cạnh huyền là 2. Quay hình tam giác ABC quanh trục BC thì được khối tròn xoay có thể tích là:
A. 2 2 3 π
B. 4 3 π
C. 2 3 π
D. 1 3 π
Cho phương trình sau: sin3x-sinx+cos2x1. Phương trình có họ nghiệm
x
π
a
+
k
2
π
3
,
k
∈
Z
hỏi giá trị của a. A.1 B.6 C.3 D.4
Đọc tiếp
Cho phương trình sau: sin3x-sinx+cos2x=1. Phương trình có họ nghiệm x = π a + k 2 π 3 , k ∈ Z hỏi giá trị của a.
A.1
B.6
C.3
D.4