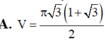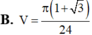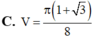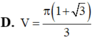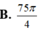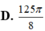Các câu hỏi tương tự
Cho tứ diện ABCD có AD
⊥
(ABC), ABC là tam giác vuông tại B. Biết BCA, ABa
3
, AD3a Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng
Đọc tiếp
Cho tứ diện ABCD có AD ⊥ (ABC), ABC là tam giác vuông tại B. Biết
BC=A, AB=a 3 , AD=3a Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng
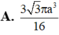
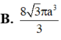
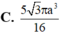
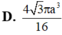
Cho tam giác ABC có BAC
120
o
. Quay tam giác ABC (bao gồm cả điểm trong tam giác) quanh đường thẳng AB ta được một khối tròn xoay. Thể tích khối tròn xoay đó bằng :
Đọc tiếp
Cho tam giác ABC có BAC= 120 o . Quay tam giác ABC (bao gồm cả điểm trong tam giác) quanh đường thẳng AB ta được một khối tròn xoay. Thể tích khối tròn xoay đó bằng :
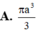
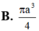
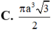
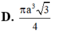
Tính thể tích khối tròn xoay sinh ra khi quay tam giác đều ABC cạnh bằng 1 quanh AB A.
3
π
4
B.
π
4
C.
π
8
D.
π
3
2
Đọc tiếp
Tính thể tích khối tròn xoay sinh ra khi quay tam giác đều ABC cạnh bằng 1 quanh AB
A. 3 π 4
B. π 4
C. π 8
D. π 3 2
Tam giác ABC vuông tại B, AB10, BC4. Gọi M,N lần lượt là trung điểm của AB, AC. Thể tích khối tròn xoay do hình thang vuông BMNC quay một vòng quanh MB là:
Đọc tiếp
Tam giác ABC vuông tại B, AB=10, BC=4. Gọi M,N lần lượt là trung điểm của AB, AC. Thể tích khối tròn xoay do hình thang vuông BMNC quay một vòng quanh MB là:
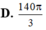
Cho tam giác đều ABC cạnh 1 và hình vuông MNPQ nội tiếp trong tam giác ABC(M
∈
AB, N
∈
AC, P,Q
∈
BC) . Gọi S là phần mặt phẳng chứa các điểm thuộc tam giác ABC nhưng không chứa các điểm thuộc hình vuông MNPQ. Thể tích của vật thể tròn xoay khi quay S quanh trục là đường thẳng qua A vuông góc với BC là:
A
.
810
-
467
3...
Đọc tiếp
Cho tam giác đều ABC cạnh 1 và hình vuông MNPQ nội tiếp trong tam giác ABC(M ∈ AB, N ∈ AC, P,Q ∈ BC) . Gọi S là phần mặt phẳng chứa các điểm thuộc tam giác ABC nhưng không chứa các điểm thuộc hình vuông MNPQ. Thể tích của vật thể tròn xoay khi quay S quanh trục là đường thẳng qua A vuông góc với BC là:
A . 810 - 467 3 24 π
B . 4 3 - 3 96 π
C . 4 3 - 3 96
D . 54 - 31 3 12 π
Cho tam giác ABC vuông tại B có AC2a, BCa khi quay tam giác ABC quay quanh cạnh góc vuông AB thì đường gấp khúc ABC tạo thành một hình nón tròn xoay có diện tích xung quanh bằng
Đọc tiếp
Cho tam giác ABC vuông tại B có AC=2a, BC=a khi quay tam giác ABC quay quanh cạnh góc vuông AB thì đường gấp khúc ABC tạo thành một hình nón tròn xoay có diện tích xung quanh bằng
Tam giác ABC vuông cân đỉnh A có cạnh huyền là 2. Quay hình tam giác ABC quanh trục BC thì được khối tròn xoay có thể tích là: A.
2
2
3
π
B.
4
3
π
C.
2
3
π
D.
1
3
π
Đọc tiếp
Tam giác ABC vuông cân đỉnh A có cạnh huyền là 2. Quay hình tam giác ABC quanh trục BC thì được khối tròn xoay có thể tích là:
A. 2 2 3 π
B. 4 3 π
C. 2 3 π
D. 1 3 π
Cho tam giác vuông cân cân ABC tại A, BC
a
2
Quay tam giác quanh đường cao AH ta được hình nón tròn xoay. Thể tích khối nón bằng
Đọc tiếp
Cho tam giác vuông cân cân ABC tại A, BC= a 2 Quay tam giác quanh đường cao AH ta được hình nón tròn xoay. Thể tích khối nón bằng
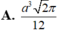
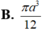
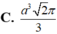
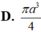
Cho tam giác ABC có Quay tam giác ABC xung quanh cạnh BC ta đuợc khối tròn xoay có thể tích V bằng:
Đọc tiếp
Cho tam giác ABC có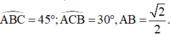 
Quay tam giác ABC xung quanh cạnh BC ta đuợc khối tròn xoay có thể tích V bằng:
