Question

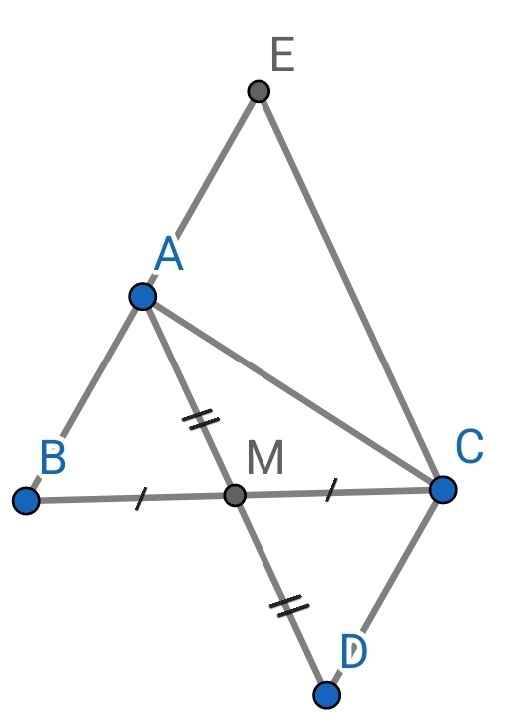
Cho tám giác ABC có M là trung điểm của BC. Trên tia đối AM lấy điểm D sao cho M là trung điểm của AD: a) Chứng Minh tam giác ABM= tam giác DCM. b) Chứng minh AB song song CD. c) Qua C kẻ đường thẳng song song với AD cắt AB kéo dài tại E. Chứng minh A là trung điểm của BE

Answer 1

 a) Do M là trung điểm của BC (gt)

⇒ BM = MC

Do M là trung điểm của AD (gt)

⇒ AM = MD

Xét ∆ABM và ∆DCM có:

AM = MD (cmt)

∠AMB = ∠CMD (đối đỉnh)

BM = MC (cmt)

⇒ ∆ABM = ∆DCM (c-g-c)

b) Do ∆ABM = ∆DCM (cmt)

⇒ ∠ABM = ∠CDM (hai góc tương ứng)

Mà ∠ABM và ∠CDM là hai góc so le trong

⇒ AB // CD

c) Do AB // CD (cmt)

⇒ ∠CAE = ∠ACD (so le trong)

∠ACE = ∠CAD (so le trong)

Xét ∆ACE và ∆CAD có:

∠ACE = ∠CAD (cmt)

AC là cạnh chung

∠CAE = ∠ACD (cmt)

⇒ ∆ACE = ∆CAD (g-c-g)

⇒ AE = CD (hai cạnh tương ứng)

Do ∆ABM = ∆DCM (cmt)

⇒ AB = CD (hai cạnh tương ứng)

Mà AE = CD (cmt)

⇒ AB = AE

Vậy A là trung điểm của BE