Question

Cho tam giác ABC có M là trung điểm AC, trên tia đối tia MB lấy điểm D sao cho MB = MD

a) CM :tam giác AMD = tam giác CMB

b) CM AB//CD

c) vẽ CN vuông góc AD (N thuộc AD) và AP vuông góc BC (P thuộc BC).CM ND = BP

d) CM N, M, P thẳng hàng

Vẽ hình hộ mình

Mình đang gấp

Answer 1

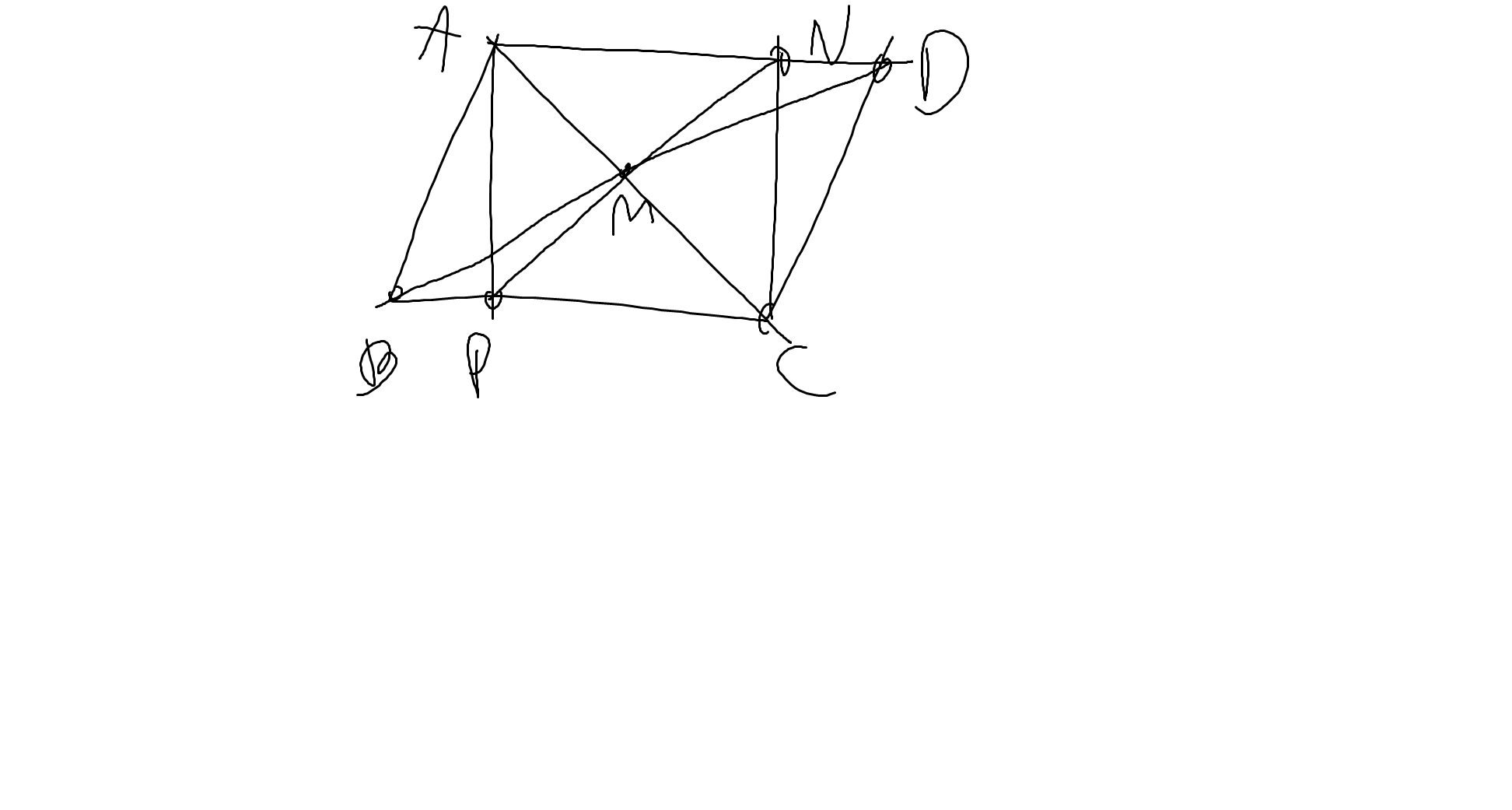
a: Xét ΔAMD và ΔCMB có

MA=MC

\(\widehat{AMD}=\widehat{CMB}\)(hai góc đối đỉnh)

MD=MB

Do đó:ΔAMD=ΔCMB

b: Xét ΔMAB và ΔMCD có

MA=MC

\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)

MB=MD

Do đó: ΔMAB=ΔMCD
=>\(\widehat{MAB}=\widehat{MCD}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AB//CD

c: ΔMAB=ΔMCD

=>AB=CD

ΔMAD=ΔMCB

=>AD=CB

Xét ΔABC và ΔCDA có

AB=CD

BC=DA

AC chung

Do đó: ΔABC=ΔCDA

=>\(\widehat{ABC}=\widehat{CDA}\)

Xét ΔBAD và ΔDCB có

BA=DC

DA=CB

BD chung

Do đó: ΔBAD=ΔDCB

=>\(\widehat{BAD}=\widehat{DCB}\)

Xét ΔAPB vuông tại P và ΔCND vuông tại N có

AB=CD

\(\widehat{ABP}=\widehat{CDN}\)

Do đó: ΔAPB=ΔCND

=>PB=ND

d: Ta có: AN+ND=AD

CP+PB=CB

mà ND=PB và AD=CB

nên AN=CP

Xét ΔMAN và ΔMCP có

MA=MC

\(\widehat{MAN}=\widehat{MCP}\)(ΔMAD=ΔMCB)

AN=CP

Do đó: ΔMAN=ΔMCP

=>\(\widehat{AMN}=\widehat{CMP}\)

=>\(\widehat{AMN}+\widehat{AMP}=180^0\)

=>N,M,P thẳng hàng