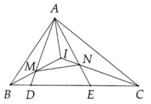
a) Tam giác ABE cân tại B có BI là phân giác nên cũng là đường cao, từ đó B I ⊥ A E . Tương tự C I ⊥ A D .
b) Từ kết quả ý a, chứng minh được I là trực tâm tam giác AMN, từ đó A I ⊥ M N

a) Tam giác ABE cân tại B có BI là phân giác nên cũng là đường cao, từ đó B I ⊥ A E . Tương tự C I ⊥ A D .
b) Từ kết quả ý a, chứng minh được I là trực tâm tam giác AMN, từ đó A I ⊥ M N
Cho tam giác ABC nhọn có cạnh BC lớn nhất . Trên BC lấy hai điểm D và E sao cho BA = BD; CA = CE.Từ B kẻ đường thẳng vuông góc với AD tại I
a) Chứng minh tam giác BAI = tam giác BDI
b) Từ C kẻ CH vuông góc với AE tại H , gọi O là giao điểm của BI và CH.Chứng minh AO là tia phân giác của góc BAC
c) Gọi M là giao điểm của BI và AE ; N là giao điểm của CH và AD.Chứng minh AO vuông góc với MN
Bài 2. Cho ABC có A = 120°. Tia phân giác của A cắt BC tại D. Tia phân giác của
ADC cắt AC tại I. Gọi H, K, E lần lượt là hình chiếu của I trên đương thẳng AB,
BC, AD. Chứng minh:
a) AC là tia phân giác của DAH .
b) IH = IK
Bài 5. Cho tam giác ABC vuông tại A. Từ một điểm K bất kì trên cạnh BC, vẽ KH
AC (HAC). Trên tia đối của tia HK lấy điểm I sao cho HI = HK. Chứng
minh:
a) Chứng minh AB //HK
b) Chứng minh KAH IAH
c) Chứng minh AKI cân
Bài 7. Cho ABC, AB = AC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao
cho AD = AE. Gọi M là giao điểm của BE và CD. Chứng minh:
a) BE = CD b) BMD = CME
c) Đường vuông góc với OE tại E cắt Ox, Oy lần lượt tại M, N. Chứng minh
MN / / AC //BD.
Bài 8. Cho xOy . Lấy các điểm A,B thuộc tia Ox sao cho OA > OB. Lấy các điểm C, D
thuộc Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC
Chứng minh.:
a) AD = BC b) ABE = CDE
c) OE là tia phân giác của góc xOy
Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt cạnh AC tại D. Trên cạnh BC lấy E sao cho BE bằng BA.
a) Chứng minh AD = DE và DE vuông góc BC.
b) Gọi I là giao điểm của AE và BD. Chứng minh: BI vuông góc AE.
c) Từ A kẻ AM song song với DE (M thuộc BD) Chứng minh: AE là phân giác góc MAD.
d) Kẻ EK vuông góc AB (K thuộc AB) Chứng minh: E, M, K thẳng hàng
Cho ABC vuông tại A, tia phân giác của góc B cắt cạnh AC tại D. Trên cạnh BC lấy E sao cho BE = BA.
a) Chứng minh: AD = DE và DE BC.
b) Gọi I là giao điểm của AE và BD. Chứng minh: BI AE.
c) Từ A kẻ AM song song với DE (M BD).
Chứng minh: AE là phân giác góc MAD.
d) Kẻ EK AB (K AB). Chứng minh: E, M, K thẳng hàng.
Cho tam giác ABC vuông tại A. Có phân giác BE. Kẻ EH vuông góc BC (H thuộc BC). Gọi K là giao điểm của các cạnh BA và EH. a) chứng minh BE vuông góc KC b) so sánh AE và EC c) Lấy D thuộc BC. Sao cho BAD=45°. Gọi I là giao điểm của BE và AD. Chứng minh I cách đều 3 cạnh của tam giác ABC. Giúp mình với ạ!!!
Cho tam giác ABC vuông tại A. Có phân giác BE. Kẻ EH vuông góc với BC (H∈BC).Gọi K là giao điểm của các cạnh BA và HE.
a) Chứng minh: BE⊥KC .
b) So sánh AE và EC.
c) Lấy D thuộc cạnh BC, Sao cho . Gọi I là giao điểm của BE và AD. Chứng minh I cách đều ba cạnh của tam giác ABC.
Mọi người ơi giúp mình vớiiii, nhớ làm cả phần c nhaaaa
Cho tam giác ABC cân tại A có A= 40°. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE. a. Tính ADE và chứng minh DE // BC b. Chứng minh : AABE =AACD c. Gọi I là giao điểm của BE VÀ CD. Chứng minh AI là đường trung tuyến của tam giác ABC
BÀI 1: Cho ∆ABC nhọn. Vẽ về phía ngoài ∆ABC các ∆ đều ABD và ACE. Gọi M là giao điểm của BE và CD. Chứng minh rằng:
a) ∆ABE = ∆ADC b) Góc BMC = 120o
Bài 2: Cho tam giác ABC có ba góc nhọn, đường cao AH. ở miền ngoài của tam giác ABC ta vẽ các tam giác vuông cân ABE và ACF đều nhận A làm đỉnh góc vuông. Kẻ EM, FN cùng vuông góc với AH (M, N thuộc AH).
a) Chứng minh: EM + HC = NH.
b) Chứng minh: EN // FM.
Bài 3:Cho cạnh hình vuông ABCD có độ dài là 1. Trên các cạnh AB, AD lấy các điểm P, Q sao cho chu vi DAPQ bằng 2.
Chứng minh rằng : Góc PCQ = 45o
Bài 4:Cho tam giác vuông cân ABC (AB = AC), tia phân giác của các góc B và C cắt AC và AB lần lượt tại E và D.
a) Chứng minh rằng: BE = CD; AD = AE.
b) Gọi I là giao điểm của BE và CD. AI cắt BC ở M, chứng minh rằng các ∆MAB; MAC là tam giác vuông cân.
c) Từ A và D vẽ các đường thẳng vuông góc với BE, các đường thẳng này cắt BC lần lượt ở K và H. Chứng minh rằng KH = KC.
Bài 5: Cho tam giác cân ABC (AB = AC ). Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB, AC lần lượt ở M, N. Chứng minh rằng:
a) DM = EN
b) Đường thẳng BC cắt MN tại trung điểm I của MN.
c) Đường thẳng vuông góc với MN tại I luôn đi qua một điểm cố định khi D thay đổi trên cạnh BC.