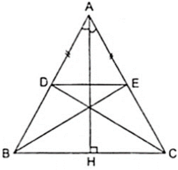
Vì Δ ABC cân tại A có AH là đường cao theo giả thiết nên AH cũng là đường phân giác của góc A.
Theo giả thiết ta có AD = AE nên Δ ADE cân tại A nên AH là đường trung trực của DE
⇒ D đối xứng với E qua AH.
Cho tam giác ABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm D, trên cạnh AC
lấy điểm E sao cho AD = AE. Chứng minh rằng:
a) D đối xứng với E qua AH.
b) Δ ADC đối xứng với Δ AEB qua AH.
Cho tam giác ABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Chứng minh rằng: Δ ADC đối xứng với Δ AEB qua AH.
Cho tam giác ABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm I, trên cạnh AC lấy điểm K sao cho AI = AK . Chứng minh rằng điểm I đối xứng với điểm K qua AH.
Cho tam giác ABC cân tại A , đường cao AH .Trên cạnh AB lấy điểm I , trên cạnh AC lấy điểm K sao cho AI=AK .Chứng minh rằng điểm I đối xứng với điểm K qua AH
Cho tam giác vuông ABC vuông tại A, đường cao AH. Trên cạnh BC lấy điểm D sao cho BD = AB, trên cạnh AC lấy điểm E sao cho AE = AH. Chứng minh rằng: CD.CH = CE.CA .
Cho tam giác ABC cân tại A. Trên tia đối của tia AB lấy điểm D, trên tia đối của tia AC lấy điểm E sao cho AD = AE. Gọi M là trung điểm của BC. Chứng minh rằng D đối xứng với E qua AM.
Cho tam giác ABC cân tại A, M là trung điểm của BC, trên tia đối của của tia AB lấy điểm E, trên tia đối của tia AC lấy điểm D sao cho AD=AE. Chứng minh rằng D và E đối xứng qua đường thẳng AM.
Cho tam giác ABC cân tại A .Trên tia đối của tia AB lấy điểm D ,trên tia đối của tia AC lấy điểm E sao cho AD=AE .Gọi M là trung điểm của BC . Chứng minh rằng D đối xứng với E qua AM
cho tam giác ABC cân tại A . trên tia đối của tia AB lấy D , trên tia đối của tia AC lấy điểm E sao cho AD = AE . gọi M là trung điểm của BC . chứng minh rằng D đôúi xứng với E qua AM
