a: Xét tứ giác ADCE có
O là trung điểm chung của AC và DE
góc ADC=90 độ
Do đó: ADCE là hình chữ nhật
b: Xét tứ giác AEDB có
AE//DB
AE=DB
Do đó: AEDB là hình bình hành
c:BD=CD=BC/2=6cm
AO=OD=10/2=5cm
AD=8cm
P=(5+5+8)/2=18/2=9cm
\(S=\sqrt{9\cdot\left(9-8\right)\left(9-5\right)\left(9-5\right)}=\sqrt{9\cdot1\cdot4\cdot4}=3\cdot2\cdot2=12\left(cm^2\right)\)
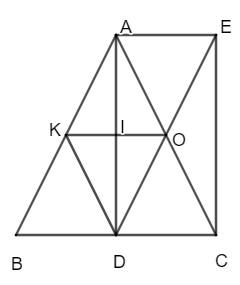
a) Tứ giác ADCE có: O là trung điểm của AC, O là trung điểm của BD
nên tứ giác ADCE là hình bình hành
Có \(\widehat{ADC}=90^\circ\)
Vậy tứ giác ADCE là hình chữ nhật.
b) AECD là hình chữ nhật \(\Rightarrow AE=DC\), AE // DC
Tam giác ABC cân tại A có AD là đường cao
\(\Rightarrow\) AD là đường trung tuyến của tam giác ABC
\(\Rightarrow\) D là trung điểm của BC \(\Rightarrow BD=DC=\dfrac{1}{2}BC\)
Xét tứ giác AEDB có: \(AE=BD\), AE // BD
Vậy tứ giác AEBD là hình bình hành.
c) Tam giác ADC vuông tại D: \(AC^2=AD^2+DC^2\) (Định lí Pi-ta-go)
\(AD=\sqrt{AC^2-DC^2}=\sqrt{10^2-6^2}=8\) (cm)
\(S_{OAD}=\dfrac{1}{2}S_{ADC}=\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot8\cdot6=12\) (cm2).
d) Tam giác ADC có: O là trung điểm của AC, I là trung điểm của AD
nên OI là đường trung bình của tam giác ADC
\(\Rightarrow\) OI // BC.
Tam giác ABC có: OK // BC, O là trung điểm của AC
\(\Rightarrow\) K là trung điểm của AB.
Tam giác ABC: O là trung điểm của AC, K là trung điểm của AB
nên OK là đường trung bình của tam giác ABC
\(\Rightarrow OK=\dfrac{1}{2}BC\)
Xét tứ giác KOCD: OK = DC, OK // DC
nên tứ giác KOCD là hình bình hành
\(\Rightarrow\) KD = OC
\(\Rightarrow KD=\dfrac{1}{2}AC\)
\(AE=DC=\dfrac{1}{2}BC\)
Để AE = DK thì AC = BC
Tam giác ABC có AC = AB = BC nên tam giác ABC đều
Vậy tam giác ABC đều thì AE = DK.














