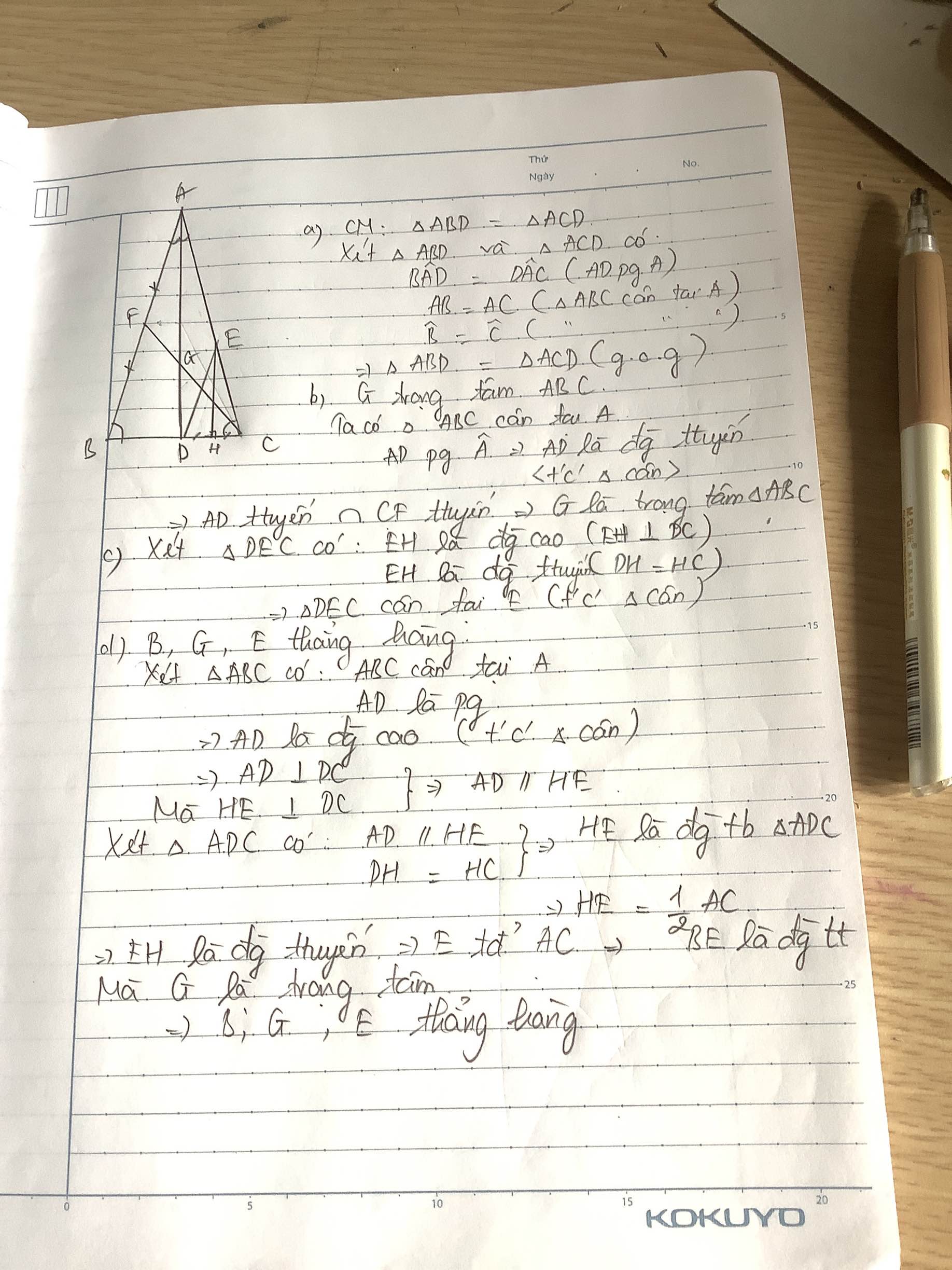Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắt cạnh BC tại D.
a) Chứng minh ΔABD = ΔACD.
b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọng tâm của tam giác ABC.
c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh ΔDEC cân.
Chứng minh ba điểm B, G, E thẳng hàng
Mình đang cần gấp giúp mình với ạ .Cảm ơn ạ
a: Xét ΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔABD=ΔACD
b: Ta có: ΔABD=ΔACD
nên BD=CD
hay D là trung điểm của BC
Xét ΔABC có
AD là đường trung tuyến ứng với cạnh BC
CF là đường trung tuyến ứng với cạnh AB
AD cắt CF tại G
DO đó: G là trọng tâm của ΔBAC
Xét ΔABC có
H là trung điểm của DC
HE//AD
Do đó: E là trung điểm của AC
Ta có: ΔADC vuông tại D
mà DE là đường trung tuyến ứng với cạnh huyền AC
nên DE=CE=AE
Xét ΔDEC có ED=EC
nên ΔDEC cân tại E
d: Ta có: G là trọng tâm của ΔBAC(cmt)
mà BE là đường trung tuyến ứng với cạnh AC
và BE,BG có điểm chung là G
nên B,E,G thẳng hàng