Question

Cho tam giác ABC cân tại A, AH là đường cao trên tia đối của tia HA lấy M qua M kẻ đường thẳng song song với BC cắt AB tại E cắt AC tại F a, CM tam giác AME= tam giác AMF b, CM MB=MC c, CM tam giác HEF

Answer 1

    

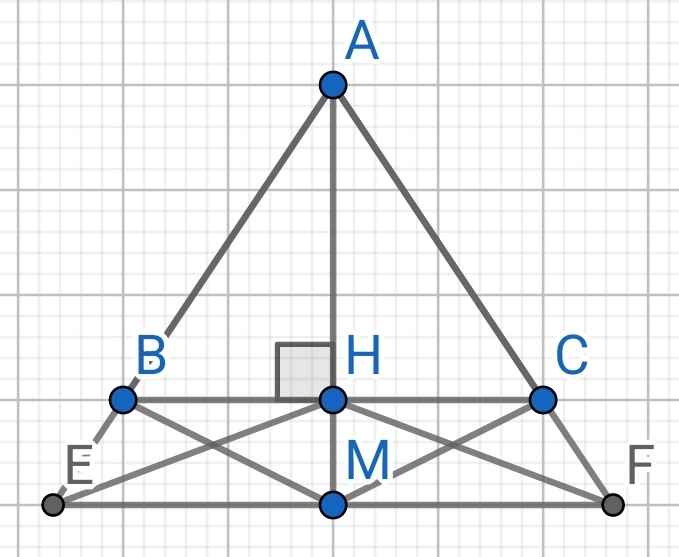
a) Do ∆ABC cân tại A (gt)

⇒ AB = AC

Xét hai tam giác vuông: ∆AHB và ∆AHC có:

AB = AC (cmt)

AH là cạnh chung

⇒ ∆AHB = ∆AHC (cạnh huyền - cạnh góc vuông)

⇒ ∠BAH = ∠CAH (hai góc tương ứng)

⇒ AH là tia phân giác của ∠BAC

Mà M ∈ AH (gt)

⇒ AM là tia phân giác của ∠BAC

⇒ ∠BAM = ∠CAM

⇒ ∠EAM = ∠FAM

Do EF // BC (gt)

AH BC (gt)

⇒ AH ⊥ EF

⇒ AM ⊥ EF

Xét hai tam giác vuông: ∆AME và ∆AMF có:

AM là cạnh chung

∠EAM = ∠FAM (cmt)

⇒ ∆AME = ∆AMF (cạnh góc vuông - góc nhọn)

b) Xét ∆ABM và ∆ACM có:

AB = AC (cmt)

∠BAM = ∠CAM (cmt)

AM là cạnh chung

⇒ ∆ABM = ∆ACM (c-g-c)

⇒ MB = MC (hai cạnh tương ứng)

c) Sửa đề: Chứng minh ∆HEF cân

Do ∆AME = ∆AMF (cmt)

⇒ ME = MF (hai cạnh tương ứng)

Xét hai tam giác vuông: ∆HEM và ∆HFM có:

HM là cạnh chung

ME = MF (cmt)

⇒ ∆HEM = ∆HFM (hai cạnh góc vuông)

⇒ HE = HF (hai cạnh tương ứng)

⇒ ∆HEF cân tại H