Question

Cho tam giác ABC (AB < AC) M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho AM = EM.

a. Chứng minh: ΔAMB = ΔMCE

b. Từ A kẻ AH vuông góc với BC. Trên tia đối của tia HA lấy điểm D sao cho HA = HD. Chứng minh: CE = BD

c. Tam giác AMD là tam giác gì? Vì sao?

Answer 1

\(\text{#TNam}\)

`a,` Xét Tam giác `AMB` và Tam giác `EMC` có:

`MA=ME (g``t)`

\(\widehat{AMB}=\widehat{CME} (\text {2 góc đối đỉnh})\)

`MB=MC (\text {M là trung điểm của BC})`

`=> \text {Tam giác AMB = Tam giác EMC (c-g-c)}`

`b,` Vì Tam giác `AMB =` Tam giác `EMC (a)`

`-> AB = CE (\text {2 cạnh tương ứng}) (1)`

Xét Tam giác `ABH` và Tam giác `DBH` có:

`HA = HD (g``t)`

\(\widehat{AHB}=\widehat{DHB}=90^0\)

`\text {BH chung}`

`=> \text {Tam giác ABH = Tam giác DBH (c-g-c)}`

`-> AB = BD (\text {2 cạnh tương ứng}) (2)`

Từ `(1)` và `(2) -> CE = BD.`

`c,` Xét Tam giác `AMH` và Tam giác `DMH` có:

`\text {MH chung}`

\(\widehat{AHM}=\widehat{DHM}=90^0\)

`HA = HD (g``t)`

`=> \text {Tam giác AMH = Tam giác DMH (c-g-c)}`

`-> MA = MD (\text {2 cạnh tương ứng})`

Xét Tam giác `AMD: MA = MD`

`-> \text {Tam giác AMD cân tại M}`

*Hoặc nếu như bạn có học rồi, thì mình có thể dùng cái này cũng được nè cậu:>.

Vì `MH` vừa là đường cao (hạ từ đỉnh `->` cạnh đối diện), vừa là đường trung tuyến.

Theo tính chất của tam giác cân `-> \text {Tam giác AMD là tam giác cân} (đpcm).`

Answer 2

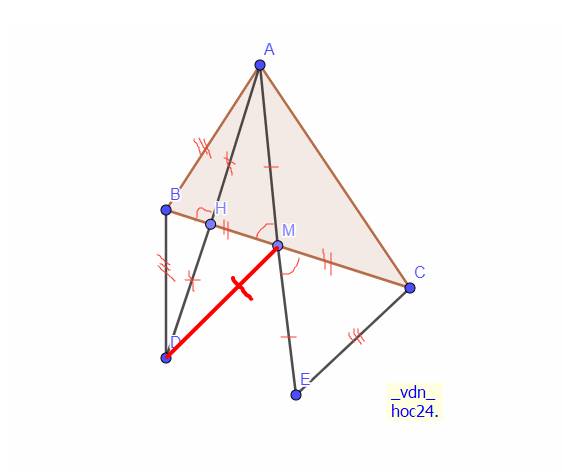
a: Xét ΔAMB và ΔEMC có

MA=ME

góc AMB=góc EMC

MB=MC

=>ΔAMB=ΔEMC

b: Xét ΔBAD có

BH vừa là đường cao, vừa là trung tuyến

=>ΔBAD cân tại B

=>BD=BA=CE

c: Xét ΔMAD có

MH vừa là đường cao, vừa là trung tuyến

=>ΔMAD cân tại M

Answer 3

a: Xét ΔMAB và ΔMEC có

MA=ME

góc AMB=góc EMC

MB=MC

=>ΔMAB=ΔMEC
b: Xét ΔBAD có

BH vừa là đường cao, vừa là trung tuyến

nên ΔBAD cân tại B

=>BA=BD=CE

c: Xét ΔMAD có

MH vừa là đường cao, vừa là trungtuyến

nên ΔMAD cân tại M