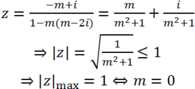Các câu hỏi tương tự
Cho số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn z + 2 + i - |z|(1+i) = 0 và |z| > 1. Tính P = a + b
A. P = -1
B. P = -5
C. P = 3
D. P = 7
Cho số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn z + 2 + i - |z|(i+1) = 0 và |z| > 1. Tính P = a + b
A. P = -1
B. P = -5
C. P = 3
D. P = 7
Cho số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn z + 2 + i - |z|(1+i) = 0 và |z| > 1. Tính P = a + b
A. P = -1
B. P = -5
C. P = 3
D. P = 7
Cho số phức
z
m
+
1
1
+
m
2
i
−
1
,
m
∈
ℝ
. Số các giá trị nguyên của m để
z
−
i...
Đọc tiếp
Cho số phức z = m + 1 1 + m 2 i − 1 , m ∈ ℝ . Số các giá trị nguyên của m để z − i < 1 là
A. 0
B. 1
C. 4
D. Vô số
Cho số phức z thỏa mãn |z - 2 - 3i| 1. Gọi M max|
z
¯
+ 1 + i|. Tính giá trị của biểu thức A.
M
2
+
m
2
28 B.
M
2
+
m
2
26 C.
M
2
+
...
Đọc tiếp
Cho số phức z thỏa mãn |z - 2 - 3i| = 1. Gọi M = max| z ¯ + 1 + i|. Tính giá trị của biểu thức
A. M 2 + m 2 = 28
B. M 2 + m 2 = 26
C. M 2 + m 2 = 24
D. M 2 + m 2 = 20
Cho số phức z a + bi(a,b
∈
ℝ
). Biết {M} biểu diễn số phức z là đường tròn
x
-
4
2
+
y
-
3
2
9
. Tìm max, min của F 4a + 3b. A.
m...
Đọc tiếp
Cho số phức z = a + bi(a,b ∈ ℝ ). Biết {M} biểu diễn số phức z là đường tròn x - 4 2 + y - 3 2 = 9 . Tìm max, min của F = 4a + 3b.
A. m a x F = 28 m i n F = 13
B. m a x F = 50 m i n F = 13
C. m a x F = 40 m i n F = 10
D. m a x F = 30 m i n F = 10
Biết {M} biểu diễn số phức Z là (d): x-y-2 0. Đặt W Z+1-i. Tìm
W
m
i
n
A.
W
m
i
n
2
B.
W
m
i
n
2 C....
Đọc tiếp
Biết {M} biểu diễn số phức Z là (d): x-y-2 = 0. Đặt W = Z+1-i. Tìm W m i n
A. W m i n = 2
B. W m i n = 2
C. W m i n = 2 2
D. W m i n = 4
Cho số phức z a + bi(a,b
∈
ℝ
). Biết tập hợp các điểm A biểu diễn hình học số phức z là đường tròn (C) có tâm I(4;3) và bán kính R 3 . Đặt M là giá trị lớn nhất, m là giá trị nhỏ nhất của F 4a + 3b -1. Tính giá trị M + m A. M + m 63 B. M + m 48 C. M + m 50 D. M + m 41
Đọc tiếp
Cho số phức z = a + bi(a,b ∈ ℝ ). Biết tập hợp các điểm A biểu diễn hình học số phức z là đường tròn (C) có tâm I(4;3) và bán kính R = 3 . Đặt M là giá trị lớn nhất, m là giá trị nhỏ nhất của F = 4a + 3b -1. Tính giá trị M + m
A. M + m = 63
B. M + m = 48
C. M + m = 50
D. M + m = 41
Cho hai số phức z,
ω
thỏa mãn
z
-
1
z
+
3
-
2
i
;
ω
z
+...
Đọc tiếp
Cho hai số phức z, ω thỏa mãn z - 1 = z + 3 - 2 i ; ω = z + m + i với m ∈ ℝ là tham số. Giá trị của m để ta luôn có là
A. 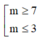
B. 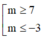
C. 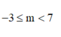
D.