Chọn C.
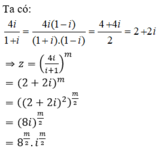
Để z là số thực khi và chỉ khi
![]()
Mà m ∈ [1;100] nên m ∈ {4;8;12;....;96;100}
![]()
giá trị m thỏa yêu cầu đề bài.
Chọn C.
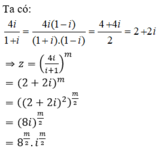
Để z là số thực khi và chỉ khi
![]()
Mà m ∈ [1;100] nên m ∈ {4;8;12;....;96;100}
![]()
giá trị m thỏa yêu cầu đề bài.
Cho số phức z = 2 + 6 i 3 - i m m nguyên dương. Có bao nhiêu giá trị 1≤ m≤ 50 để z là số thuần ảo?
A. 26.
B. 25.
C. 24.
D. 50.
Cho số phức z = 2 + 6 i 3 - i m , m nguyên dương. Có bao nhiêu giá trị m ∈ [1;50] để z là số thuần ảo?
A. 26.
B. 25.
C. 24.
D. 50.
Có bao nhiêu giá trị nguyên của m để có đúng 2 số phức z thỏa mãn z - ( m - 1 ) + i = 8 và z - 1 + i = z - 2 + 3 i .
A. 130
B. 66
C. 65
D. 131
Cho số phức z = m + 1 1 + m 2 i − 1 , m ∈ ℝ . Số các giá trị nguyên của m để z − i < 1 là
A. 0
B. 1
C. 4
D. Vô số
Trên tập ℂ , cho số phức z = i + m i - 1 với m là tham số thực khác -1. Tìm tất cả các giá trị của tham số m để z. z ¯ = 5
A. m = -3
B. m = 1
C. m = ± 2
D. m = ± 3
Trên tập ℂ , cho số phức z = i + m i - 1 với m là tham số thực khác -1. Tìm tất cả các giá trị của tham số m để z. z ¯ = 5
A. m = -3
B. m = 1
C. m = ± 2
D. m = ± 3
Cho số phức z thỏa mãn |z| = 1 m 2 + 2m, trong đó m là số thực dương tùy ý. Biết rằng với mỗi m, tập hợp các điểm biểu diễn số phức w = (2i+1)(i+ z ¯ )-5+3i là một đường tròn bán kính r. Tìm giá trị nhỏ nhất của r
A . 3 2
B . 2 3
C . 3 5
D . 5 3
Cho số phức z = a + b i a , b ∈ R Biết tập hợp các điểm A biểu diễn hình học số phức z là đường tròn (C) có tâm I(4;3) và bán kính R=3 Đặt M là giá trị lớn nhất, m là giá trị nhỏ nhất của F = 4a+3b-1 Tính giá trị M+m
A. M + m = 63
B. M + m = 48
C. M + m = 50
D. M + m = 41
Cho số phức z = a + bi(a,b ∈ ℝ ). Biết tập hợp các điểm A biểu diễn hình học số phức z là đường tròn (C) có tâm I(4;3) và bán kính R = 3 . Đặt M là giá trị lớn nhất, m là giá trị nhỏ nhất của F = 4a + 3b -1. Tính giá trị M + m
A. M + m = 63
B. M + m = 48
C. M + m = 50
D. M + m = 41