Chọn A.
Phương pháp: Áp dụng định lý Viets và điều kiện một số phức là số thực thì phần ảo phải bằng 0.

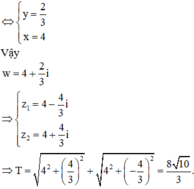
Chọn A.
Phương pháp: Áp dụng định lý Viets và điều kiện một số phức là số thực thì phần ảo phải bằng 0.

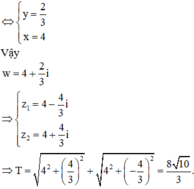
Cho số phức z thỏa mãn z − 1 + i + z + 2 − 3 i = 5 và w = z − i . Gọi T là giá trị lớn nhất của w . Tìm T.
A. T = 5
B. T = 2 5
C. T = 2 2
D. T = 2 5
Cho số phức z thỏa mãn z − 1 + i + z + 2 − 3 i = 5 và w = z − i . Gọi T là giá trị lớn nhất của |w|. Tìm T.
A. T = 5
B. T = 2 5
C. T = 2 2
D. T = 2 5
Cho các số phức z, w khác 0 và thỏa mãn |z-w| = 2|z| = |w|. Phẩn thực của số phức u = z w là:
A. a = 1 4
B. a = 1
C. a = 1 8
D. a = - 1 8
Cho các số phức z và w thỏa mãn ( 3 - i ) z = z w - 1 + 1 - i . Tìm GTLN của T = w + i .
A. 2 2
B. 3 2 2
C. 2
D. 1 2
Cho số phức z thỏa mãn 2 + i z + 2 1 + 2 i 1 + i = 7 + 8 i . Kí hiệu a, b lần lượt là phần thực và phần ảo của số phức w = z + 1 + i . Tính P = a 2 + b 2
A. P = 5
B. P = 7
C. P = 13
D. P = 25
Cho số phức w và hai số thực a, b. Biết z 1 =w+2i và z 2 =2w-3 là hai nghiệm phức của phương trình z 2 + a z + b = 0 . Tính T= | z 1 | + | z 2 |
A. T=2 13
B. T= 2 97 3
C. T= 2 85 3
D. T=4 13
Cho các số phức z, w thỏa mãn z − 5 + 3 i = 3 , i w + 4 + 2 i = 2. Tìm giá trị lớn nhất của biểu thức T = 3 i z + 2 w
A. 554 + 5
B. 578 + 13
C. 578 + 5
D. 554 + 13
Cho các số phức z và w thỏa mãn 2 + i z = z w + 1 - i . Tìm giá trị lớn nhất của T = w + 1 - i
A. 4 2 3
B. 2 3
C. 2 2 3
D. 2
Cho các số phức z và w thỏa mãn 2 + i z = z w + 1 - i . Tìm giá trị lớn nhất của T = w + 1 - i
A. 4 2 3
B. 2 3
C. 2 2 3
D. 2