Chọn đáp án A
Ta có
![]()
![]()
Đặt t = 2 x > 0 thì phương trình đã cho trở thành t 2 - 2 m . t + m + 2 = 0 *
Để phương trình đã cho có hai nghiệm dương phân biệt khi và chỉ khi phương trình (*) có hai nghiệm t 1 , t 2 lớn hơn 1.
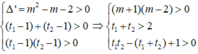
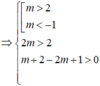
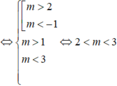
![]()
Chọn đáp án A
Ta có
![]()
![]()
Đặt t = 2 x > 0 thì phương trình đã cho trở thành t 2 - 2 m . t + m + 2 = 0 *
Để phương trình đã cho có hai nghiệm dương phân biệt khi và chỉ khi phương trình (*) có hai nghiệm t 1 , t 2 lớn hơn 1.
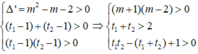
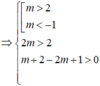
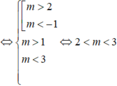
![]()
Cho phương trình 4 x − m .2 x + 1 + m + 2 = 0 , m là tham số. Gọi S là tập hợp các giá trị của m sao cho phương trình trên có hai nghiệm dương phân biệt. Biết S là một khoảng có dạng (a;b) tính a-b
A. 1
B. 3
C. 4
D. 2
Gọi S = − ∞ ; a b (với a b là phân số tối giản, a ∈ Z , b ∈ N * ) là tập hợp tất cả các giá trị của tham số m sao cho phương trình 2 x 2 + m x + 1 = x + 3 có hai nghiệm phân biệt. Tính B = a 2 − b 3 .
A. B = 334.
B. B = − 440 .
C. B = 1018.
D. B = 8.
Cho phương trình m - 1 log 1 2 2 x - 2 2 + 4 m - 5 log 1 2 1 x - 2 + 4 m - 4 = 0 (với m là tham số). Gọi S = a , b là tập hợp các giá trị của m để phương trình có nghiệm trên đoạn 5 2 ; 4 . Tính a + b
A. 7 3
B. - 2 3
C. - 3
D. 1034 237
Cho phương trình
2
log
4
2
x
2
−
x
+
2
m
−
4
m
2
+
log
1
2
x
2
+
m
x
−
2
m
2
=
0
Biết
S
=
a
;
b
∪
c
;
d
,
a
<
b
<
c
<
d
là tập hợp các giá trị của tham số m để phương trình đã cho có hai nghiệm phân biệt
x
1
,
x
2
thỏa mãn
x
1
2
+
x
2
2
>
1
. Tính giá trị biểu thức
A. A = 1
B. A = 2
C. A = 0
D. A = 3
Cho phương trình:
( m − 1 ) log 1 2 2 x − 2 2 + 4 m − 5 log 1 2 1 x − 2 + 4 m − 4 = 0 (với m là tham số). Gọi S = [ a ; b ] là tập các giá trị của m để phương trình có nghiệm trên đoạn 5 2 ; 4 . Tính a+b.
A. 7 3
B. − 2 3
C. − 3
D. 1034 237
Cho phương trình 2 log 4 2 x 2 - x + 2 m - 4 m 2 + log 1 2 x 2 + m x - 2 m 2 = 0 . Biết rằng S = a ; b ∪ c ; d , a < b < c < d là tập hợp các giá trị của tham số m để phương trình đã cho có hai nghiệm phân biệt x 1 , x 2 thỏa x 1 2 + x 2 2 > 1 . Tính giá trị biểu thức A = a + b + 5c + 2d
A. A = 1
B. A = 2
C. A = 0
D. A = 3
Cho phương trình m ln 2 x + 1 - x + 2 - m ln x + 1 - x - 2 = 0 1 . Tập tất cả giá trị của tham số m để phương trình 1 có các nghiệm, trong đó có hai nghiệm phân biệt thỏa mãn 0 < x 1 < 2 < 4 < x 2 là khoảng a ; + ∞ . Khi đó, a thuộc khoảng
A. (3,8;3,9)
B. (3,7;3,8)
C. (3,6;3,7)
D. (3,5;3,6)
Cho S là tập hợp các giá trị thực của tham số m để phương trình 2 − x + 1 − x = m + x − x 2 có hai nghiệm phân biệt. Tổng các số nguyên trong S bằng
A. 11
B. 0
C. 5
D. 6
Cho phương trình e m . cos x - sin x - e 2 1 - sin x = 2 - sin x - m . cos x với m là tham số thực. Gọi S là tập hợp tất cả các giá trị của m để phương trình có nghiệm. Khi đó S=( - ∞ ; a ] ∪ [ b ; + ∞ ). Tính T=10a+20b
A. 10 3
B . 0
C. 19
D. -1