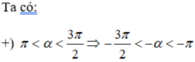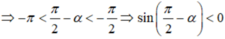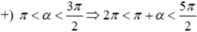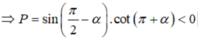Các câu hỏi tương tự
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM α, π/2 α π, A(1; 0). Gọi
M
2
là điểm đối xứng với M qua trục Ox. Số đo của cung
A
M
3
là A. π - α + k2π, k ∈ Z B. α + π/2 + k2π, k ∈ Z C. α - π + k2π, k ∈ Z D. -α + k2π, k ∈ Z
Đọc tiếp
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, π/2 < α < π, A(1; 0). Gọi M 2 là điểm đối xứng với M qua trục Ox. Số đo của cung A M 3 là
A. π - α + k2π, k ∈ Z B. α + π/2 + k2π, k ∈ Z
C. α - π + k2π, k ∈ Z D. -α + k2π, k ∈ Z
Cho sinα=3/5 và 0<α<π/2. Khi đó, giá trị của A= sin(π−α)+cos(π+α)+cos(−α) là gì?
Online chờ gấp, đa tạ các vị!
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM α, π α 3π/2, A(1; 0). Gọi
M
2
là điểm đối xứng với M qua trục Ox. Số đo của cung A
M
2
là A. α - π + k2π, k ∈ Z B. π - α + k2π, k ∈ Z C. 2π - α + k2π, k ∈ Z D. 3π/2 - α + k2π, k ∈ Z
Đọc tiếp
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, π < α < 3π/2, A(1; 0). Gọi M 2 là điểm đối xứng với M qua trục Ox. Số đo của cung A M 2 là
A. α - π + k2π, k ∈ Z B. π - α + k2π, k ∈ Z
C. 2π - α + k2π, k ∈ Z D. 3π/2 - α + k2π, k ∈ Z
Cho π < α 3π/2. Xác định dấu của các giá trị lượng giác sau sin(π/2 + α)
Cho 0 < α < π/2. Xác định dấu của các giá trị lượng giác
Cho sinα = 8/17, sinβ = 15/17 với 0 < α < π/2, 0 < β <π/2. Chứng minh rằng: α + β = π/2
Cho
π
2
α
π
Xác định dấu của các biểu thức sau:
A
sin
π
2
+
α
A. A 0 B. A 0 C. A 1 D. A -1
Đọc tiếp
Cho π 2 < α < π Xác định dấu của các biểu thức sau: A = sin π 2 + α
A. A > 0
B. A < 0
C. A > 1
D. A < -1
Cho π < α 3π/2. Xác định dấu của các giá trị lượng giác sau cos(α - π/2)
Cho π < α 3π/2. Xác định dấu của các giá trị lượng giác sau cot(α + π)