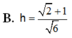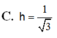Các câu hỏi tương tự
Trong không gian Oxyz, cho mặt cầu (S):
(
x
+
1
)
2
+
(
y
-
1
)
2
+
(
z
-
2
)
2
9
và mặt phẳng (P):...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): ( x + 1 ) 2 + ( y - 1 ) 2 + ( z - 2 ) 2 = 9 và mặt phẳng (P): 2x-2y+z+14=0. Gọi M ( a ; b ; c ) là điểm thuộc mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) lớn nhất. Tính T = a + b + c .
![]()
![]()
![]()
![]()
Cho hình nón đỉnh I và đường tròn đáy tâm O. Bán kính đáy bằng chiều cao của hình nón. Giả sử khoảng cách từ trung điểm của IO tới một đường sinh bất kì là
2
. Hai điểm A, B nằm trên đường tròn tâm O sao cho AB 1/2. Tính thể tích khối tứ diện IABO A.
63
12
B.
7
6
C.
255
12...
Đọc tiếp
Cho hình nón đỉnh I và đường tròn đáy tâm O. Bán kính đáy bằng chiều cao của hình nón. Giả sử khoảng cách từ trung điểm của IO tới một đường sinh bất kì là 2 . Hai điểm A, B nằm trên đường tròn tâm O sao cho AB = 1/2. Tính thể tích khối tứ diện IABO
A. 63 12
B. 7 6
C. 255 12
D. 5 4
Trong không gian Oxyz, cho hai điểm A(2; 0; 0), B(0; 0; 8) và điểm C sao cho AC → = (0; 6; 0). Tính khoảng cách từ trung điểm I của BC đến đường thẳng OA.
Cho (P): x - y - z - 3 0,
d
:
x
-
2
4
3
z
5
. Gọi
A
d
∩
P
và M là trung điểm OA. Tính khoảng cách h từ M tới (P):
Đọc tiếp
Cho (P): x - y - z - 3 = 0, d : x - 2 = 4 3 = z 5 . Gọi A = d ∩ P và M là trung điểm OA. Tính khoảng cách h từ M tới (P):
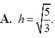
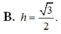
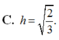
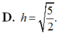
Trong không gian Oxyz, cho điểm A(1;−3;0) và mặt cầu (S):
(
x
-
2
)
2
+
(
y
+
6
)
2
+
z
2
50
tâm I. Xét các điểm M thuộc (S) sao cho góc
∠
A
M...
Đọc tiếp
Trong không gian Oxyz, cho điểm A(1;−3;0) và mặt cầu (S): ( x - 2 ) 2 + ( y + 6 ) 2 + z 2 = 50 tâm I. Xét các điểm M thuộc (S) sao cho góc ∠ A M I lớn nhất, M luôn thuộc mặt phẳng có phương trình là
![]()
![]()
![]()
![]()
Cho
P
:
2
x
-
y
+
2
z
-
4
0
;
A
1
;
2
;
-
1
;
B
∈
P
với
x
B
3
,
y...
Đọc tiếp
Cho P : 2 x - y + 2 z - 4 = 0 ; A 1 ; 2 ; - 1 ; B ∈ P với x B = 3 , y B = 2 3 . Gọi M là trung điểm của AB. Tính khoảng cách h từ M tới (P).
![]()
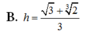
![]()
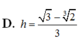
Tìm điểm M thuộc tia Ox sao cho khoảng cách từ M tới mặt phẳng (P) bằng
3
với
P
:
2
+
x
+
y
+
z
0
.
Đọc tiếp
Tìm điểm M thuộc tia Ox sao cho khoảng cách từ M tới mặt phẳng (P) bằng 3 với P : 2 + x + y + z = 0 .
![]()
![]()
![]()
![]()
Cho
P
:
2
x
-
y
+
2
z
-
1
0
, A bất kì thuộc (P). Gọi M là trung điểm OA ( O là gốc tọa độ). Tính khoảng cách h từ M tới mặt phẳng (P).
Đọc tiếp
Cho P : 2 x - y + 2 z - 1 = 0 , A bất kì thuộc (P). Gọi M là trung điểm OA ( O là gốc tọa độ). Tính khoảng cách h từ M tới mặt phẳng (P).
![]()
![]()
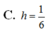
![]()
Cho hàm số
y
2
x
-
1
x
-
1
có đồ thị (C) và điểm I (1; 2). Điểm M( a; b) ; a 0 thuộc (C) sao cho tiếp tuyến tại M của (C) vuông góc với đường thẳng IM. Giá trị a+ b bằng A. 3 B . 4 C. 5 D. 6
Đọc tiếp
Cho hàm số y = 2 x - 1 x - 1 có đồ thị (C) và điểm I (1; 2). Điểm M( a; b) ; a> 0 thuộc (C) sao cho tiếp tuyến tại M của (C) vuông góc với đường thẳng IM.
Giá trị a+ b bằng
A. 3
B . 4
C. 5
D. 6