Các câu hỏi tương tự
Cho đường tròn (O; R) có đường kính AB, lấy điểm M thuộc đường tròn (O) sao cho AMBM. Tiếp tuyến tại A của đường tròn (O) cắt tia OM tại S. Đường cao AH của tam giác SAO (H thuộc SO) cắt đường tròn tại D. Kẻ đường kính DE của đường tròn (O). Gọi r là bán kính đường tròn nội tiếp tam giác SAD. Chứng minh M là tâm đường tròn nội tiếp tam giác SAD và tính chiều dài đoạn thẳng AE theo R, r.
Đọc tiếp
Cho đường tròn (O; R) có đường kính AB, lấy điểm M thuộc đường tròn (O) sao cho AM<BM. Tiếp tuyến tại A của đường tròn (O) cắt tia OM tại S. Đường cao AH của tam giác SAO (H thuộc SO) cắt đường tròn tại D. Kẻ đường kính DE của đường tròn (O). Gọi r là bán kính đường tròn nội tiếp tam giác SAD. Chứng minh M là tâm đường tròn nội tiếp tam giác SAD và tính chiều dài đoạn thẳng AE theo R, r.
Cho đường tròn (O;R) có đường kính BC. Lấy A thuộc (O) sao cho AB < AC, vẽ đường cao AH của tam giác ABC.
a) Chứng minh: AH.BC=AB.AC.
b) Tiếp tuyến tại A của (O) cắt đường thẳng BC tại M. Chứng minh rằng:
MA^2=MB.MC.
c) Kẻ HE vuông góc với AB (E thuộc AB) và HF vuông góc với AC ( F thuộc AC). Chứng minh AM // EF.
1) Cho đường tròn tâm O, bán kính R, đường kính AB. Điểm M thuộc (O) sao cho AmR a. Chứng minh tam giác AMB vuông. Tính MB theo Rb. Vẽ MN vuông góc AB (N thuộc đường tròn tâm O) . Tiếp tuyến tại M cắt đường thẳng AB tại I. Chứng minh góc MOI góc NOI và IN là tiếp tuyến của (O) c. Lấy điểm E thuộc cung nhỏ MN, vẽ tiếp tuyến tại E với (O) cắt IM, IN lần lượt tại C và F. Tính chu vi tam giác ICF theo R
Đọc tiếp
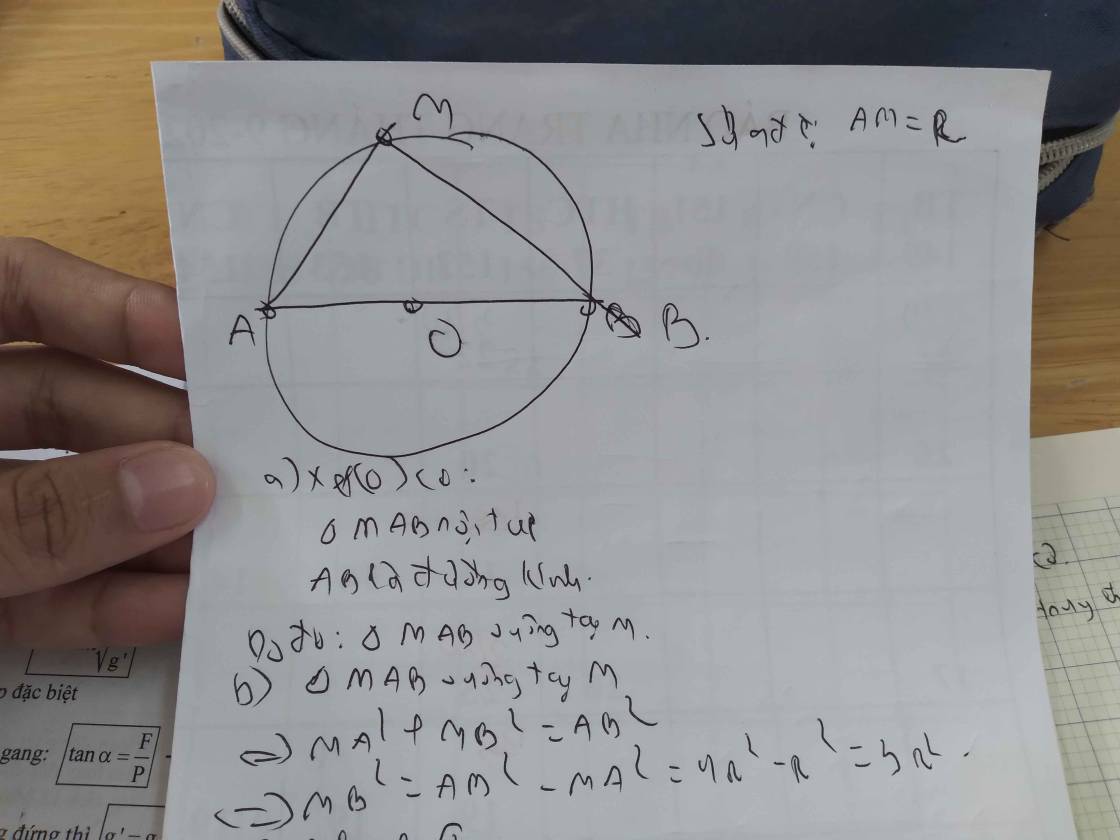
1) Cho đường tròn tâm O, bán kính R, đường kính AB. Điểm M thuộc (O) sao cho Am=R
a. Chứng minh tam giác AMB vuông. Tính MB theo R
b. Vẽ MN vuông góc AB (N thuộc đường tròn tâm O) . Tiếp tuyến tại M cắt đường thẳng AB tại I. Chứng minh góc MOI= góc NOI và IN là tiếp tuyến của (O)
c. Lấy điểm E thuộc cung nhỏ MN, vẽ tiếp tuyến tại E với (O) cắt IM, IN lần lượt tại C và F. Tính chu vi tam giác ICF theo R
cho đường tròn (O,R) đường kính AB. trên tia đối của tia ab lấy điểm M (M khác A),từ M kẻ tiếp tuyến MC với đướng tròn (O,R) (C là tiếp điểm). kẻ CH vuông góc với AB ( H thuộc AB)
a)chứng minh tam giác OCM là tam giác vuông tính độ dài đoạn thẳng CH khi biết R6cm,AM4cm.
b) vẽ dây AD của đường tròn (O,R) vuông góc vs OC tại I.chứng minh MCAADC
c)dây AD cắt CH theo thứ tự P,Q.chứng minh AI*AQAP*AD
Đọc tiếp
cho đường tròn (O,R) đường kính AB. trên tia đối của tia ab lấy điểm M (M khác A),từ M kẻ tiếp tuyến MC với đướng tròn (O,R) (C là tiếp điểm). kẻ CH vuông góc với AB ( H thuộc AB)
a)chứng minh tam giác OCM là tam giác vuông tính độ dài đoạn thẳng CH khi biết R=6cm,AM=4cm.
b) vẽ dây AD của đường tròn (O,R) vuông góc vs OC tại I.chứng minh MCA=ADC
c)dây AD cắt CH theo thứ tự P,Q.chứng minh AI*AQ=AP*AD
Cho đường tròn (O; R) đường kính AB và điểm M thuộc đường tròn (O) (MA MA, M khác A và B). Kẻ MH vuông góc với AB tại H.a) Chứng minh tam giác ABM vuông. Giả sử MA 3cm, MB 4cm, hãy tính MH.b) Tiếp tuyến tại A của đường tròn (O) cắt tia BM ở C. Gọi N là trung điểm của AC. Chứng minh đường thẳng NM là tiếp tuyến của đường tròn (O).c) Tiếp tuyến tại B của (O) cắt đường thẳng MN tại D. Chứng minh: NA.BD R2d) Chứng minh: OC vuông góc AD
Đọc tiếp
Cho đường tròn (O; R) đường kính AB và điểm M thuộc đường tròn (O) (MA < MA, M khác A và B). Kẻ MH vuông góc với AB tại H.
a) Chứng minh tam giác ABM vuông. Giả sử MA = 3cm, MB = 4cm, hãy tính MH.
b) Tiếp tuyến tại A của đường tròn (O) cắt tia BM ở C. Gọi N là trung điểm của AC. Chứng minh đường thẳng NM là tiếp tuyến của đường tròn (O).
c) Tiếp tuyến tại B của (O) cắt đường thẳng MN tại D. Chứng minh: NA.BD = R2
d) Chứng minh: OC vuông góc AD
Cho đường tròn (O; R) có đường kính AB. Vẽ tiếp tuyến Ax với đường tròn (O; R), trên đường tròn (O; R) lấy điểm C sao cho .
a/ Chứng minh: Tam giác ABC vuông và tính độ dài AC, BC theo R.
b/ Tia BC cắt Ax tại M, kẻ CH AB tại H. Chứng minh: MC.BC = AH.AB
c/ Gọi I là trung điểm của CH, tia BI cắt AM tại E. Chứng minh: E là trung điểm của AM và EC là tiếp tuyến của đường tròn (O; R).
cho đường tròn (o,r) đường kính ab. trên tia đối của tia ab lấy điểm m (m khác a), từ m kẻ tiếp tuyến mc với đg tròn (o,r)(c là tiếp điểm). kẻ ch vuông góc với ab ( h thuộc ab) a)chứng minh tam giác ocm là tam giác vuông tính độ dài đoạn thẳng ch khi bt r6cm,am4cm. b) vẽ dây ad của đg tròn (o,r)vuông góc vs oc tại i.chứng minh mcaadc. c)dây ad cắt ch theo thứ tự p,q.chứng minh ai.aqap.ad
Đọc tiếp
cho đường tròn (o,r) đường kính ab. trên tia đối của tia ab lấy điểm m (m khác a), từ m kẻ tiếp tuyến mc với đg tròn (o,r)(c là tiếp điểm). kẻ ch vuông góc với ab ( h thuộc ab) a)chứng minh tam giác ocm là tam giác vuông tính độ dài đoạn thẳng ch khi bt r=6cm,am=4cm. b) vẽ dây ad của đg tròn (o,r)vuông góc vs oc tại i.chứng minh mca=adc. c)dây ad cắt ch theo thứ tự p,q.chứng minh ai.aq=ap.ad
LAMF GIÚP MÌNH CÂU D cho đường tròn (O; R) đường kính AB và điểm M thuộc đường tròn (O) (MA MA, M khác A và B). Kẻ MH vuông góc với AB tại H.a) Chứng minh tam giác ABM vuông. Giả sử MA 3cm, MB 4cm, hãy tính MH.b) Tiếp tuyến tại A của đường tròn (O) cắt tia BM ở C. Gọi N là trung điểm của AC. Chứng minh đường thẳng NM là tiếp tuyến của đường tròn (O).c) Tiếp tuyến tại B của (O) cắt đường thẳng MN tại D. Chứng minh: NA.BD R2d) Chứng minh: OC vuông góc AD
Đọc tiếp
LAMF GIÚP MÌNH CÂU D cho đường tròn (O; R) đường kính AB và điểm M thuộc đường tròn (O) (MA < MA, M khác A và B). Kẻ MH vuông góc với AB tại H.
a) Chứng minh tam giác ABM vuông. Giả sử MA = 3cm, MB = 4cm, hãy tính MH.
b) Tiếp tuyến tại A của đường tròn (O) cắt tia BM ở C. Gọi N là trung điểm của AC. Chứng minh đường thẳng NM là tiếp tuyến của đường tròn (O).
c) Tiếp tuyến tại B của (O) cắt đường thẳng MN tại D. Chứng minh: NA.BD = R2
d) Chứng minh: OC vuông góc AD
Cho đường tròn (O; R) đường kính AB và điểm M thuộc đường tròn (O) (MA MA, M khác A và B). Kẻ MH vuông góc với AB tại H.a) Chứng minh tam giác ABM vuông. Giả sử MA 3cm, MB 4cm, hãy tính MH.b) Tiếp tuyến tại A của đường tròn (O) cắt tia BM ở C. Gọi N là trung điểm của AC. Chứng minh đường thẳng NM là tiếp tuyến của đường tròn (O).c) Tiếp tuyến tại B của (O) cắt đường thẳng MN tại D. Chứng minh: NA.BD R2d) Chứng minh: OC vuông góc AD
Đọc tiếp
Cho đường tròn (O; R) đường kính AB và điểm M thuộc đường tròn (O) (MA < MA, M khác A và B). Kẻ MH vuông góc với AB tại H.
a) Chứng minh tam giác ABM vuông. Giả sử MA = 3cm, MB = 4cm, hãy tính MH.
b) Tiếp tuyến tại A của đường tròn (O) cắt tia BM ở C. Gọi N là trung điểm của AC. Chứng minh đường thẳng NM là tiếp tuyến của đường tròn (O).
c) Tiếp tuyến tại B của (O) cắt đường thẳng MN tại D. Chứng minh: NA.BD = R2
d) Chứng minh: OC vuông góc AD