Các câu hỏi tương tự
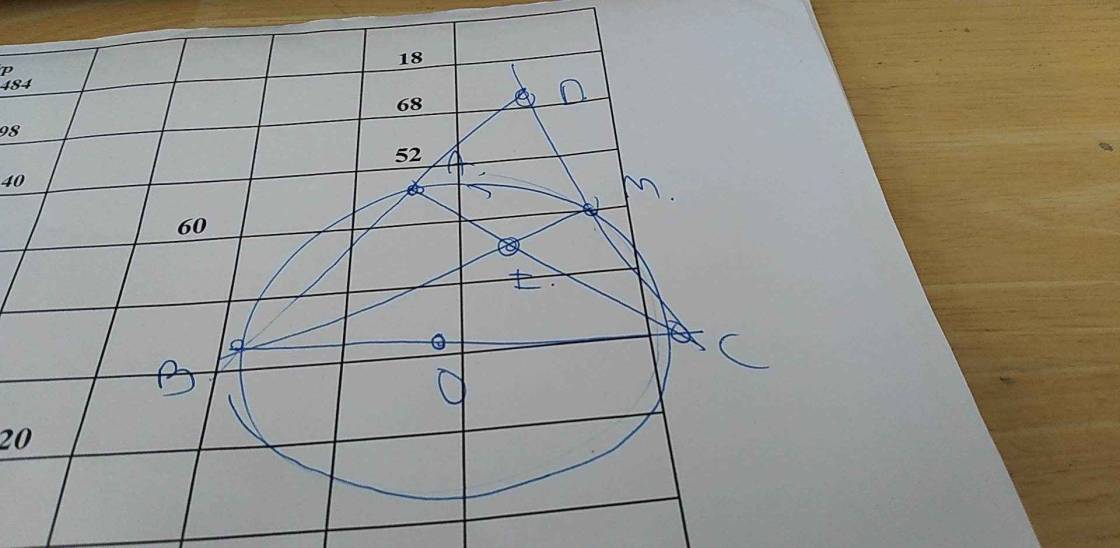
Cho nửa đường tròn tân O , đường kính BC= 2R và một điểm A trên nửa đường tròn ấy sao cho BA= R ,M là điểm trên cung AC . MB cắt AC tại I tia BA cắt CM tai D.
a) chứng minh : tam giác AOM đều .
b)chứng minh tứ giác AIMD nội tiếp đường tròn
c) tính diện tích hình quạt ADC theo R .
d) tính góc ADI=?.
e) cho góc ABM= 45 độ . Tính độ dài đoạn thẳng AD theo R.
Cho nửa đường tròn (O;R), đường kính BC và điểm A thuộc nửa đường tròn, M là điểm trên cung nhỏ AC, 2 đoạn thẳng cắt nhau tại I, tia BA cắt CM tại D a)CM tứ giác AIMD nội tiếp b)CM AI.AC=BI.IM c)CM góc ADI = nửa góc AOB Mn giúp mình với mai thi giữa kì rồi ạ !!!!!!
Cho nửa đường tròn tâm O đường kính AB lấy điểm c thuộc nửa đường tròn sao cho AC = R.căn2. N là một điểm trên cung nhỏ BC AN cắt BC tại I tia AC cắt BN tại D a. ACO là tam giác gì b . tính độ dài BC theo R c. Tính số đo góc BAC và số đo góc CDI
Cho nửa đường tròn tâm O đường kính AB = 2R và tia tiếp tuyến Ax cùng phía với nửa đường tròn đối với AB. Từ điểm M trên Ax kẻ tiếp tuyến thứ hai MC với nửa đường tròn (C là tiếp điểm). AC cắt OM tại E; MB cắt nửa đường tròn (O) tại D (D khác B).
a) Chứng minh: AMDE là tứ giác nội tiếp đường tròn.
b) Chứng minh : góc ADE=góc ACO
Cho nửa đường tròn tâm O đường kính AB = 2R và tia tiếp tuyến Ax cùng phía với nửa đường tròn đối với AB. Từ điểm M trên Ax kẻ tiếp tuyến thứ hai MC với nửa đường tròn (C là tiếp điểm). AC cắt OM tại E; MB cắt nửa đường tròn (O) tại D (D khác B).
a) Chứng minh: AMDE là tứ giác nội tiếp đường tròn.
b) Chứng minh : góc ADE=góc ACO
Cho nửa đường tròn tâm O đường kính AB 2R. Trên nửa mật phắng chứa nửa đường tròn tâm O có bờ là AB vẽ tia tiếp tuyến Ax. Từ điểm M trên Ax kẻ tiếp tuyến thứ hai MC với nửa đường tròn (C là tiếp điểm). AC cắt OM tại E; MB cắt nửa đường tròn (O) tại D (D khác B). a. Chứng minh: AMDE là tứ giác nội tiếp đường tròn. b. Chứng minh: MA2 MD.MB c. Vẽ CH vuông góc với AB (H ∈ AB). Chứng minh rằng MB đi qua trung điểm của CH
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB = 2R. Trên nửa mật phắng chứa nửa đường tròn tâm O có bờ là AB vẽ tia tiếp tuyến Ax. Từ điểm M trên Ax kẻ tiếp tuyến thứ hai MC với nửa đường tròn (C là tiếp điểm). AC cắt OM tại E; MB cắt nửa đường tròn (O) tại D (D khác B).
a. Chứng minh: AMDE là tứ giác nội tiếp đường tròn.
b. Chứng minh: MA2 = MD.MB
c. Vẽ CH vuông góc với AB (H ∈ AB). Chứng minh rằng MB đi qua trung điểm của CH
cho nửa đường tròn tâm O đường kính AB bằng 2r gọi C và D là hai điểm trên nửa đường tròn sao cho C thuộc cung AD và góc COD bằng 120 độ AD cắt BC tại E AC cắt BD tại F .chứng minh rằng:
a/ 4 điểm CDEF cùng thuộc một đường tròn
b/ tính r đường tròn đi qua CDEF qua r
Bài 4: Cho nửa đường tròn (O; R) đường kính AB. Điểm C di động trên nửa đường tròn (C khác A, B), gọi M là điểm chính giữa cung AC, BM cắt AC tại H và cắt tia tiếp tuyến Ax của nửa đường tròn (O) tại K, AM cắt BC tại D. a) Chứng minh tứ giác DMHC nội tiếp và HM. HB HA.HC b) Chứng minh ABD cân đỉnh B c) Chứng minh KD là tiếp tuyến của (B; BA). d) Tứ giác AKDH là hình gì? Vì sao? e) Đường tròn ngoại tiếp BHD cắt đường tròn (B; BA) tại N. Chứng minh A, C, N thẳng hàng.
Đọc tiếp
Bài 4: Cho nửa đường tròn (O; R) đường kính AB. Điểm C di động trên nửa đường tròn (C khác A, B), gọi M là điểm chính giữa cung AC, BM cắt AC tại H và cắt tia tiếp tuyến Ax của nửa đường tròn (O) tại K, AM cắt BC tại D. a) Chứng minh tứ giác DMHC nội tiếp và HM. HB = HA.HC b) Chứng minh ABD cân đỉnh B c) Chứng minh KD là tiếp tuyến của (B; BA). d) Tứ giác AKDH là hình gì? Vì sao? e) Đường tròn ngoại tiếp BHD cắt đường tròn (B; BA) tại N. Chứng minh A, C, N thẳng hàng.
Cho nửa đường tròn tâm o bán kính BC. A nằm trên nửa đường tròn M là một điểm trên cung AC BM cắt AC tại i tia BA cắt BM tại i chứng ming rằng
a. Tứ giác AIMD nội tiếp đường tròn
b. Góc AID bằng góc AOM