Các câu hỏi tương tự
Câu 1:(0,5đ)Liệt kê các phần tử của tập hợp A {x ∈ N/15 ≤ x ≤ 19}Câu 2: (3đ) thực hiện phép tínha. 2.(72 – 2.32) – 60b. 27.63 + 27.37c. l-7l + (-8) + l-11l + 2d. 568 – 34 {5.l9 – ( 4-1)2l + 10}Câu 3: ( 2,5 điểm ) Tìm số nguyên xa) 2x + 3 52 : 5b) 105 – ( x + 7) 27 : 25Câu 4 (1 điểm): Học sinh lớp 6B khi xếp hàng 2, hàng 4, hàng 8 đều vừa đủ hàng. Biết số học sinh lớp đó trong khoảng 30 đến 38. Tính số học sinh của lớp 6B.Câu 5:(1 điểm) Khi nào thì M là trung điểm của đoạn thẳng AB? Vẽ...
Đọc tiếp
Câu 1:(0,5đ)
Liệt kê các phần tử của tập hợp A = {x ∈ N/15 ≤ x ≤ 19}
Câu 2: (3đ) thực hiện phép tính
a. 2.(72 – 2.32) – 60
b. 27.63 + 27.37
c. l-7l + (-8) + l-11l + 2
d. 568 – 34 {5.l9 – ( 4-1)2l + 10}
Câu 3: ( 2,5 điểm ) Tìm số nguyên x
a) 2x + 3 = 52 : 5
b) 105 – ( x + 7) = 27 : 25
Câu 4 (1 điểm): Học sinh lớp 6B khi xếp hàng 2, hàng 4, hàng 8 đều vừa đủ hàng. Biết số học sinh lớp đó trong khoảng 30 đến 38. Tính số học sinh của lớp 6B.
Câu 5:(1 điểm) Khi nào thì M là trung điểm của đoạn thẳng AB? Vẽ hình minh họa.
Câu 6: ( 2 điểm )Vẽ tia Ox, trên Ox lấy điểm A và B sao cho OA= 4cm, OB = 8cm.
a. Trong 3 điểm O, A, B điểm nào nằm giữa 2 điểm còn lại. Vì sao? . So sánh OA và AB
b. A có phải là trung điểm của OB không? Vì sao ?
Cho hai đường thẳng
d
:
x
+
y
-
1
0
và
d
:
x
+
y
-
5
0
. Phép tịnh tiến theo vecto
u
→
biến đường thẳng d thành d. Khi đó, độ dài bé nhất của
u
→
là bao nhiêu? A.
2
2
B. 5...
Đọc tiếp
Cho hai đường thẳng d : x + y - 1 = 0 và d ' : x + y - 5 = 0 . Phép tịnh tiến theo vecto u → biến đường thẳng d thành d'. Khi đó, độ dài bé nhất của u → là bao nhiêu?
A. 2 2
B. 5
C. 2
D. 4 2
Trong không gian Oxyz, cho đường thẳng d:
x
-
2
1
y
-
1
-
2
z
-
1
2
và hai điểm A(3;2;1), B(2;0;4). Gọi...
Đọc tiếp
Trong không gian Oxyz, cho đường thẳng d: x - 2 1 = y - 1 - 2 = z - 1 2 và hai điểm A(3;2;1), B(2;0;4). Gọi ∆ là đường thẳng qua A, vuông góc với d sao cho khoảng cách từ B đến ∆ là nhỏ nhất. Gọi u → = 2 ; b ; c là một VTCP của ∆. Khi đó , u → bằng
A. 17
B. 5
C. 6
D. 3
Câu1: Cho số xyz chia hết cho 37. Chứng minh rằng số yzx chia hết cho 37Câu2: có hay không 2 số tự nhiên x và y sao cho: 2002x + 5648y 203 253 ?Câu3: từ 1 đến 1000 có bao nhiêu số chia hết cho 2, có bao nhiêu số chia hết cho 5 ?Câu4: tích ( n+2002 ).( n+2003 ) có chia hết cho 2 không? giải thích?Câu5: tìm x,y để số 30xy chia hết cho cả 2 và 3, và chia cho 5 dư 2Câu6: Viết số tự nhiên nhỏ nhất có 5 chữ số, tận cùng bằng 6 và chia hết cho 9. Câu7: a, Có bao nhiêu số có 2 chữ số chia hết cho...
Đọc tiếp
Câu1: Cho số xyz chia hết cho 37. Chứng minh rằng số yzx chia hết cho 37
Câu2: có hay không 2 số tự nhiên x và y sao cho: 2002x + 5648y = 203 253 ?
Câu3: từ 1 đến 1000 có bao nhiêu số chia hết cho 2, có bao nhiêu số chia hết cho 5 ?
Câu4: tích ( n+2002 ).( n+2003 ) có chia hết cho 2 không? giải thích?
Câu5: tìm x,y để số 30xy chia hết cho cả 2 và 3, và chia cho 5 dư 2
Câu6: Viết số tự nhiên nhỏ nhất có 5 chữ số, tận cùng bằng 6 và chia hết cho 9.
Câu7:
a, Có bao nhiêu số có 2 chữ số chia hết cho 9 ?
b, Tìm tổng các số có 2 chữ số chia hết cho 9 .
Câu8: chứng minh rằng:
a, 102002 + 8 chia hết cho cả 9 và 2 .
b, 102004 + 14 chia hết cho cả 2 và 3 .
Câu9: tìm tập hợp A các số tự nhiên x là ước của 75 và là bội của 3.
Câu10: tìm các số tự nhiên x,y sao cho: ( 2x + 1 ). ( y - 5 ) = 12
Câu11: số ababab là số nguyên tố hay hợp số ?
Câu12: chứng minh rằng số abcabc chia hết ít nhất cho 3 số nguyên tố.
Câu13: chứng minh rằng: 2001 . 2002 . 2003 . 2004 + 1 là hợp số.
Câu14: tướng Trần Hưng Đạo đánh tan 50 vạn quân nguyên năm abcd, biết : a là số tự nhiên nhỏ nhất khác 0 ; b là số nguyên tố nhỏ nhất; c là hợp số chẵn lớn nhất có một chữ số; d là số tự nhiên liền sau số nguyên tố lẻ nhỏ nhất. Vậy abcd là năm nào ?
Câu15: cho p là một số nguyên tố lớn hơn 3 và 2p + 1 cũng là một số nguyên tố, thì 4p + 1 là số nguyên tố hay hợp số ? vì sao ?
Câu16: tìm 3 số tự nhiên liên tiếp có tích bằng 19 656.
Câu17: tìm số tụ nhiên n biết rằng: 1 + 2 + 3 +...+ n = 1275
Câu18: tìm số chia và thương của một phép chia, biết số bị chia là 150 và số dư là 7.
Câu19: tìm giao của 2 tập hợp A và B :
a, A là tập hợp các số tự nhiên chia hết cho 3. B là tập hợp các số tự nhiên chia hết cho 9.
b, A là tập hợp các số nguyên tố. B là tâp hợp các hợp số.
c, A là tập hợp các số nguyên tố bé hơn 10. B là tập hợp các chữ số lẻ.
--------- Hết---------
GIÚP VỚI, MAI NỘP RỒI.
Khi tính nguyên hàm
∫
x
-
3
x
+
1
d
x
, bằng cách đặt
u
x
+
1
ta được nguyên hàm nào? A.
∫
2
u
u
2
-...
Đọc tiếp
Khi tính nguyên hàm ∫ x - 3 x + 1 d x , bằng cách đặt u = x + 1 ta được nguyên hàm nào?
A. ∫ 2 u u 2 - 4 d u
B. ∫ u 2 - 4 d u
C. ∫ 2 u 2 - 4 d u
D. ∫ u 2 - 3 d u
Khi tính nguyên hàm
∫
x
-
3
x
+
1
d
x
, bằng cách đặt
u
x
+
1
ta được nguyên hàm nào A.
∫
2
u
2
-
4
d
u
B. ...
Đọc tiếp
Khi tính nguyên hàm ∫ x - 3 x + 1 d x , bằng cách đặt u = x + 1 ta được nguyên hàm nào
A. ∫ 2 u 2 - 4 d u
B. ∫ u 2 - 4 d u
C. ∫ u 2 - 3 d u
D. ∫ 2 u u 2 - 4 d u
Tính
I
∫
x
s
inx
d
x
,
đặt
u
x
,
d
v
s
inx dx
.
Khi đó I biến đổi thành A.
I
−
x
c
osx-
∫
c
osx
d
x
B.
I
−
x
c
osx
+...
Đọc tiếp
Tính I = ∫ x s inx d x , đặt u = x , d v = s inx dx . Khi đó I biến đổi thành
A. I = − x c osx- ∫ c osx d x
B. I = − x c osx + ∫ c osx d x ,
C. I = x c osx + ∫ c osx d x ,
D. I = − x sin x + ∫ c osx d x
Cho hai đường thẳng
d
:
x
+
y
−
1
0
và
d
:
x
+
y
−
5
0
. Phép tịnh tiến theo vecto
u
→
biến đường thẳng d thành d’. Khi đó, độ dài bé nhất của là bao nhiêu? A. 5 B.
2
C.
2
2...
Đọc tiếp
Cho hai đường thẳng d : x + y − 1 = 0 và d ' : x + y − 5 = 0 . Phép tịnh tiến theo vecto u → biến đường thẳng d thành d’. Khi đó, độ dài bé nhất của là bao nhiêu?
A. 5
B. 2
C. 2 2
D. 4 2
Câu 1: (2,5 điểm) Cho biểu thức:a) Rút gọn A.b) Tính giá trị của biểu thức A tại x thỏa mãn: 2x2 + x 0c) Tìm x để A 1/2d) Tìm x nguyên để A nguyên dương.Câu 2: (1điểm)a) Biểu diễn tập nghiệm của mỗi bất phương trình sau trên trục số: x ≥ -1 ; x 3.b) Cho a b, so sánh – 3a +1 với – 3b + 1.HD: a b -3a -3bCâu 3: (1,5 điểm) Một người đi xe đạp từ A đến B với vận tốc trung bình 15km/h. Lúc về, người đó chỉ đi với vận tốc trung bình 12km/h, nên thời gian về nhiều hơn thời gian đi l...
Đọc tiếp
Câu 1: (2,5 điểm) Cho biểu thức:
![]()
a) Rút gọn A.
b) Tính giá trị của biểu thức A tại x thỏa mãn: 2x2 + x = 0
c) Tìm x để A = 1/2
d) Tìm x nguyên để A nguyên dương.
Câu 2: (1điểm)
a) Biểu diễn tập nghiệm của mỗi bất phương trình sau trên trục số: x ≥ -1 ; x < 3.
b) Cho a < b, so sánh – 3a +1 với – 3b + 1.
HD: a < b => -3a > -3b
Câu 3: (1,5 điểm) Một người đi xe đạp từ A đến B với vận tốc trung bình 15km/h. Lúc về, người đó chỉ đi với vận tốc trung bình 12km/h, nên thời gian về nhiều hơn thời gian đi là 45 phút. Tính độ dài quãng đường AB (bằng kilômet).
HD: Đổi 45’ = ¾ h, quãng đường AB = S => S = vt hay S/15 = S/12+3/4
![]()
Câu 4: (1,0 điểm) Cho tam giác ABC có AD là phân giác trong của góc A. Tìm x trong hình vẽ sau với độ dài cho sẵn trong hình.
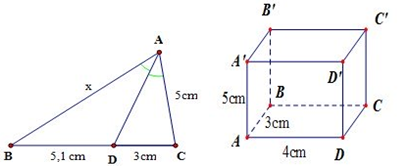
Câu 5: (1,5 điểm)
a. Viết công thức tính thể tích của hình hộp chữ nhật.
b. Áp dụng: Tính thể tích của hình hộp chữ nhật với AA’ = 5cm, AB = 3cm, AD = 4cm (hình vẽ trên).
Câu 6:(2,5 điểm) Cho tam giác ABC vuông tại A có AB = 6cm; AC = 8cm. Kẻ đường cao AH.
a) Chứng minh: ∆ABC và ∆HBA đồng dạng với nhau.
b) Chứng minh: AH2 = HB.HC.
c) Tính độ dài các cạnh BC, AH.