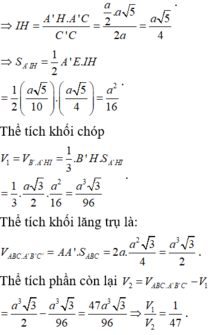Các câu hỏi tương tự
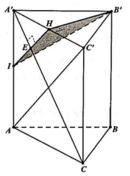
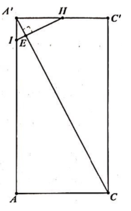
Cho lăng trụ tam giác đều ABC.A’B’C’ cạnh đáy bằng a, chiều cao bằng 2a. Mặt phẳng (P) qua B¢ và vuông góc AC¢ chia lăng trụ thành hai khối. Biết thể tích của hai khối là
V
1
,
V
2
với
V
1
V
2
. Tỉ số
V
1
V
2
: A.
1...
Đọc tiếp
Cho lăng trụ tam giác đều ABC.A’B’C’ cạnh đáy bằng a, chiều cao bằng 2a. Mặt phẳng (P) qua B¢ và vuông góc AC¢ chia lăng trụ thành hai khối. Biết thể tích của hai khối là V 1 , V 2 với V 1 < V 2 . Tỉ số V 1 V 2 :
A. 1 23
B. 1 47
C. 1 11
D. 1 7
Cho lăng trụ tam giác đều ABC.ABC có cạnh đáy bằng a chiều cao bằng 2a. Mặt phẳng (P) qua B và vuông góc AC chia lăng trụ thành hai khối. Biết thể tích của hai khối là
V
1
và
V
2
với
V
1
V
2
. Tỉ số
V
1
V
2
bằng A. ...
Đọc tiếp
Cho lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng a chiều cao bằng 2a. Mặt phẳng (P) qua B' và vuông góc A'C chia lăng trụ thành hai khối. Biết thể tích của hai khối là V 1 và V 2 với V 1 < V 2 . Tỉ số V 1 V 2 bằng
A. 1 7
B. 1 11
C. 1 23
D. 1 47
Cho lăng trụ tam giác
A
B
C
.
A
B
C
. Mặt phẳng đi qua A, B và trung điểm M của cạnh
C
C
chia lăng trụ thành 2 phần có thể tích
V
1
,
V
2
V
1...
Đọc tiếp
Cho lăng trụ tam giác A B C . A ' B ' C ' . Mặt phẳng đi qua A, B và trung điểm M của cạnh C C ' chia lăng trụ thành 2 phần có thể tích V 1 , V 2 V 1 > V 2 . Tỉ số V 1 V 2 là
A. 4
B. 2
C. 5
D. 3
Cho lăng trụ tam giác đều ABC.A’B’C’ cạnh đáy bằng a; chiều cao bằng 2a . Mặt phẳng (P) qua B’ và vuông góc A’C chia lăng trụ thành hai khối. Tính khoảng cách từ điểm A đến (P). A.
9
a
5
10
B.
7
a
5
5
C.
7
a
5...
Đọc tiếp
Cho lăng trụ tam giác đều ABC.A’B’C’ cạnh đáy bằng a; chiều cao bằng 2a . Mặt phẳng (P) qua B’ và vuông góc A’C chia lăng trụ thành hai khối. Tính khoảng cách từ điểm A đến (P).
A. 9 a 5 10
B. 7 a 5 5
C. 7 a 5 10
D. 3 a 5 10
Cho lăng trụ tam giác ABC.ABC. Mặt phẳng đi qua A,B và trung điểm M của cạnh chia lăng trụ thành 2 phần có thể tích
V
1
,
V
2
V
1
V
2
. Tỉ số
V
1
V...
Đọc tiếp
Cho lăng trụ tam giác ABC.A'B'C'. Mặt phẳng đi qua A,B và trung điểm M của cạnh ![]() chia lăng trụ thành 2 phần có thể tích
V
1
,
V
2
V
1
>
V
2
. Tỉ số
V
1
V
2
là
chia lăng trụ thành 2 phần có thể tích
V
1
,
V
2
V
1
>
V
2
. Tỉ số
V
1
V
2
là
A. 4
B. 2
C. 5
D. 3
Cho lăng trụ tam giác đều tất cả các cạnh bằng a nội tiếp trong một hình trụ (T). Gọi
V
1
,
V
2
lần lượt là thể tích của khối trụ (T) và khối lăng trụ đã cho. Tính tỉ số
V
1
V
2
A.
V
1
V
2...
Đọc tiếp
Cho lăng trụ tam giác đều tất cả các cạnh bằng a nội tiếp trong một hình trụ (T). Gọi V 1 , V 2 lần lượt là thể tích của khối trụ (T) và khối lăng trụ đã cho. Tính tỉ số V 1 V 2
A. V 1 V 2 = 4 3 π 9
B. V 1 V 2 = 4 3 π 3
C. V 1 V 2 = 3 π 9
D. V 1 V 2 = 3 π 3
Cho lăng trụ tam giác đều tất cả các cạnh bằng a nội tiếp trong một hình trụ (T). Gọi V1, V2 lần lượt là thể tích của khối trụ (T) và khối lăng trụ đã cho. Tính tỉ số
V
1
V
2
Đọc tiếp
Cho lăng trụ tam giác đều tất cả các cạnh bằng a nội tiếp trong một hình trụ (T). Gọi V1, V2 lần lượt là thể tích của khối trụ (T) và khối lăng trụ đã cho. Tính tỉ số V 1 V 2
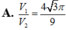
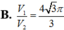
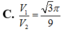
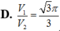
Cho khối trụ có bán kính đáy bằng r và chiều cao bằng h. Cắt khối trụ bằng mặt phẳng (P) song song với trục và cách trục một khoảng bằng
r
2
2
. Mặt phẳng (P) chia khối trụ thành hai phần. Gọi
V
1
là thể tích của phần chứa tâm của đường tròn đáy và
V
2
thể tích của phần không chứa tâm của đường tròn đáy, tính tỉ số ...
Đọc tiếp
Cho khối trụ có bán kính đáy bằng r và chiều cao bằng h. Cắt khối trụ bằng mặt phẳng (P) song song với trục và cách trục một khoảng bằng r 2 2 . Mặt phẳng (P) chia khối trụ thành hai phần. Gọi V 1 là thể tích của phần chứa tâm của đường tròn đáy và V 2 thể tích của phần không chứa tâm của đường tròn đáy, tính tỉ số V 1 V 2 .
A. V 1 V 2 = 3 π − 2 π − 2
B. V 1 V 2 = π − 2 3 π + 2
C. V 1 V 2 = 3 + 2 2
D. V 1 V 2 = 3 π + 2 π - 2
Cho khối trụ có bán kính đáy bằng r và chiều cao bằng h. Cắt khối trụ bằng mặt phẳng (P) song song với trục và cách trục một khoảng bằng
r
2
2
. Mặt phẳng (P) chia khối trụ thành hai phần. Gọi
V
1
là thể tích của phần chứa tâm của đường tròn đáy và
V
2
thể tích của phần không chứa tâm của đường tròn đáy, tính tỉ số
V
1...
Đọc tiếp
Cho khối trụ có bán kính đáy bằng r và chiều cao bằng h. Cắt khối trụ bằng mặt phẳng (P) song song với trục và cách trục một khoảng bằng r 2 2 . Mặt phẳng (P) chia khối trụ thành hai phần. Gọi V 1 là thể tích của phần chứa tâm của đường tròn đáy và V 2 thể tích của phần không chứa tâm của đường tròn đáy, tính tỉ số V 1 V 2 .
A. V 1 V 2 = 3 π − 2 π − 2
B. V 1 V 2 = π − 2 3 π + 2
C. V 1 V 2 = 3 + 2 2
D. V 1 V 2 = 3 π + 2 π − 2