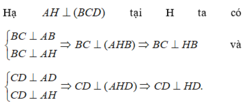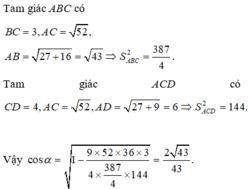Các câu hỏi tương tự
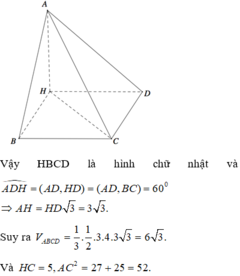
Cho khối tứ diện ABCD có
B
C
3
;
C
d
4
;
A
B
C
^
B
C
D
^
A
D
C
^
90
∘
Góc giữa hai đường thẳng AD...
Đọc tiếp
Cho khối tứ diện ABCD có B C = 3 ; C d = 4 ; A B C ^ = B C D ^ = A D C ^ = 90 ∘ Góc giữa hai đường thẳng AD và BC bằng 60 độ Côsin góc giữa hai mặt phẳng (ABC) và (ACD) bằng
A. 2 43 43
B. 43 86
C. 4 43 43
D. 43 43
Cho khối tứ diện ABCD có BC3, CD4,
A
B
C
^
B
C
D
^
A
D
C
^
90
°
. Góc giữa hai đường thẳng AD và BC bằng
60
0
. Côsin góc giữa hai mặt phẳng (ABC...
Đọc tiếp
Cho khối tứ diện ABCD có BC=3, CD=4, A B C ^ = B C D ^ = A D C ^ = 90 ° . Góc giữa hai đường thẳng AD và BC bằng 60 0 . Côsin góc giữa hai mặt phẳng (ABC) và (ACD) bằng
A. 2 43 43
B. 43 86
C. 4 43 43
D. 43 43
Cho khối tứ diện ABCD có
B
C
3
,
C
D
4
,
∠
A
B
C
∠
B
C
D
∠
A
D
C
90
0
. Góc giữa hai đường thẳng AD và BC bằng . Côsin góc giữa hai mặt phẳng
A
B
C
v
à...
Đọc tiếp
Cho khối tứ diện ABCD có B C = 3 , C D = 4 , ∠ A B C = ∠ B C D = ∠ A D C = 90 0 . Góc giữa hai đường thẳng AD và BC bằng . Côsin góc giữa hai mặt phẳng A B C v à A C D bằng
A. 43 86
B. 43 43
C. 2 43 43
D. 4 43 43
Trong không gian Oxyz, cho tam giác nhọn ABC có H(2;2;1),
K
−
8
3
;
4
3
;
8
3
, O lần lượt là hình chiếu vuông góc của A, B, C trên các cạnh BC, AC, AB. Đường thẳng d qua A và vuông góc với mặt phẳng (ABC) có phư...
Đọc tiếp
Trong không gian Oxyz, cho tam giác nhọn ABC có H(2;2;1), K − 8 3 ; 4 3 ; 8 3 , O lần lượt là hình chiếu vuông góc của A, B, C trên các cạnh BC, AC, AB. Đường thẳng d qua A và vuông góc với mặt phẳng (ABC) có phương trình là
A. d : x 1 = y − 6 − 2 = z − 6 2
B. d : x − 8 3 1 = y − 2 3 − 2 = z + 2 3 2
C. d : x + 4 9 1 = y − 17 9 − 2 = z − 19 9 2
D. d : x + 4 1 = y + 1 − 2 = z − 1 2
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB1,BC2,AA3. Côsin góc giữa hai mặt phẳng (ACD′) và (BCD′A′) bằng A.
2
10
7
B.
3
7
C.
3
35
35
D.
910
35
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=1,BC=2,AA'=3. Côsin góc giữa hai mặt phẳng (ACD′) và (BCD′A′) bằng
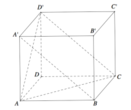
A. 2 10 7
B. 3 7
C. 3 35 35
D. 910 35
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB1,BC2,AA
3
. Côsin góc giữa hai mặt phẳng (ACD′) và (BCD′A′) bằng A.
57
19
B.
4
19
19
C.
6
4
D.
10...
Đọc tiếp
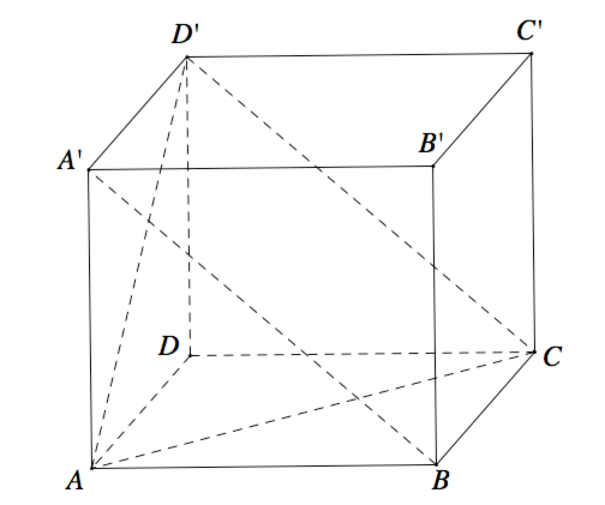
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=1,BC=2,AA'= 3 . Côsin góc giữa hai mặt phẳng (ACD′) và (BCD′A′) bằng
A. 57 19
B. 4 19 19
C. 6 4
D. 10 4
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
(
P
)
:
2
y
-
z
+
3
0
và điểm A(2;0;0). Mặt phẳng
(
α
)
đi qua A, vuông góc với (P), cách gốc tọa độ O một khoảng bằng...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( P ) : 2 y - z + 3 = 0 và điểm A(2;0;0). Mặt phẳng ( α ) đi qua A, vuông góc với (P), cách gốc tọa độ O một khoảng bằng 4 3 và cắt các tia Oy, Oz lần lượt tại các điểm B, C khác O. Thể tích khối tứ diện OABC bằng:
A. 8.
B. 16.
C. 8 3
D. 16 3
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
P
:
2
y
−
z
+
3
0
và điểm
A
2
;
0
;
0
.
Mặt phẳng
α
đi qua A, vuông góc với
P
,
cách gốc tọa độ O một khoảng bằng
4...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 2 y − z + 3 = 0 và điểm A 2 ; 0 ; 0 .
Mặt phẳng α đi qua A, vuông góc với P , cách gốc tọa độ O một khoảng bằng 4 3 và cắt các tia Oy, Oz lần lượt tại các điểm B, C khác O. Thể tích khối tứ diện OABC bằng
A. 8
B. 16
C. 8 3 .
D. 16 3 .
Trong không gian với hệ toạ độ Oxyz, cho tam giác nhọn ABC có H(2;2;1),K(
-
8
3
;
4
3
;
8
3
),O lần lượt là chân đường cao hạ từ các đỉnh A,B,C lên các cạnh BC,CA,AB. Đường thẳng qua A và vuông góc với mặt phẳng (ABC) là A.
x
+
4
1
y
+...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho tam giác nhọn ABC có H(2;2;1),K( - 8 3 ; 4 3 ; 8 3 ),O lần lượt là chân đường cao hạ từ các đỉnh A,B,C lên các cạnh BC,CA,AB. Đường thẳng qua A và vuông góc với mặt phẳng (ABC) là
A. x + 4 1 = y + 1 - 2 = z - 1 2
B. x + 4 9 1 = y - 17 9 - 2 = z - 19 9 2
C. x - 8 3 1 = y - 2 3 - 2 = z + 2 3 2
D. x 1 = y - 6 - 2 = z - 6 2