Các câu hỏi tương tự
Cho khối trụ có hai đáy là hình tròn (O;R) và
O
;
R
,
O
O
4
R
. Trên đường tròn tâm O lấy (O) lấy hai điểm A, B sao cho
A
B
R
3
. Mặt phẳng (P) đi qua A, B cắt OO’ và tạo với đáy một góc bằng
60
°
. (P) cắt khối trụ theo...
Đọc tiếp
Cho khối trụ có hai đáy là hình tròn (O;R) và O ' ; R , O O ' = 4 R . Trên đường tròn tâm O lấy (O) lấy hai điểm A, B sao cho A B = R 3 . Mặt phẳng (P) đi qua A, B cắt OO’ và tạo với đáy một góc bằng 60 ° . (P) cắt khối trụ theo thiết diện là một phần của elip. Diện tích thiết diện đó bằng:
A. 4 π 3 − 3 2 R 2
B. 2 π 3 + 3 4 R 2
C. 4 π 3 + 3 2 R 2
D. 2 π 3 − 3 4 R 2
Cho khối trụ có hai đáy là hai hình tròn
O
;
R
,
O
;
R
,
O
O
4
R
.
Trên đường tròn (O;R) lấy hai điểm A, B sao cho
A
B
R...
Đọc tiếp
Cho khối trụ có hai đáy là hai hình tròn O ; R , O ; R ' , O O ' = 4 R . Trên đường tròn (O;R) lấy hai điểm A, B sao cho A B = R 3 . Mặt phẳng (P) đi qua A, B cắt OO' và tạo với đáy một góc bằng 60 ° . (P) cắt khối trụ theo thiết diện là một phần của elip. Diện tích thiết diện đó bằng:
A. 4 π 3 − 3 2 R 2 .
B. 2 π 3 − 3 4 R 2 .
C. 2 π 3 + 3 4 R 2 .
D. 4 π 3 + 3 2 R 2 .
Cho khối trụ có hai đáy là hai hình tròn (O;R) và(O’;R),OO’4R. Trên đường tròn (O;R) lấy hai điểm A, B sao cho
A
B
R
3
. Mặt phẳng (P) đi qua A, B cắt đoạn OO’ và tạo với đáy một góc bằng 60 độ (P) cắt khối trụ theo thiết diện là một phần của hình elip. Diện tích thiết diện đó bằng A.
4
π
3
-...
Đọc tiếp
Cho khối trụ có hai đáy là hai hình tròn (O;R) và(O’;R),OO’=4R. Trên đường tròn (O;R) lấy hai điểm A, B sao cho A B = R 3 . Mặt phẳng (P) đi qua A, B cắt đoạn OO’ và tạo với đáy một góc bằng 60 độ (P) cắt khối trụ theo thiết diện là một phần của hình elip. Diện tích thiết diện đó bằng
A. 4 π 3 - 3 2 R 2
B. 2 π 3 - 3 4 R 2
C. 2 π 3 + 3 4 R 2
D. 4 π 3 + 3 2 R 2
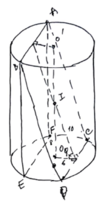
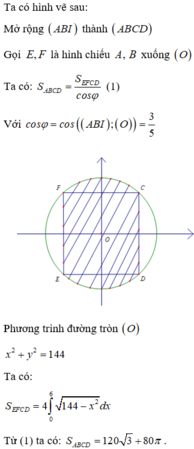
Một khối gỗ hình trụ với bán kính đáy bằng 6 và chiều cao bằng 8. Trên một đường tròn đáy nào đó ta lấy hai điểm A,B sao cho cung
A
B
có số đo
120
°
. Người ta cắt khúc gỗ bởi một mặt phẳng đi qua A, B và tâm của hình trụ (tâm của hình trụ là trung điểm của đoạn nối tâm hai đáy) để được thiết diện như hình vẽ. Tính diện tích S của thiết diện thu được. A. S 20
π
+30
3
B. S 20
π
+...
Đọc tiếp
Một khối gỗ hình trụ với bán kính đáy bằng 6 và chiều cao bằng 8. Trên một đường tròn đáy nào đó ta lấy hai điểm A,B sao cho cung A B có số đo 120 ° . Người ta cắt khúc gỗ bởi một mặt phẳng đi qua A, B và tâm của hình trụ (tâm của hình trụ là trung điểm của đoạn nối tâm hai đáy) để được thiết diện như hình vẽ. Tính diện tích S của thiết diện thu được.
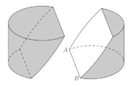
A. S = 20 π +30 3
B. S = 20 π +25 3
C. S = 12 π +18 3
D. S = 20 π
Cho khối trụ có hai đáy là hai hình tròn (O;R), (O;R), OO4R. Trên đường tròn (O;R), lấy hai điểm A, B sao cho
A
B
R
3
Mặt phẳng (P) đi qua A, B cắt OO và tạo với đáy một góc bằng
60
0
. (P) cắt khối trụ theo thiết diện là một phần của elip. Diện tích thiết diện đó bằng A.
4
π
3...
Đọc tiếp
Cho khối trụ có hai đáy là hai hình tròn (O;R), (O;R'), OO'=4R. Trên đường tròn (O;R), lấy hai điểm A, B sao cho A B = R 3 Mặt phẳng (P) đi qua A, B cắt OO' và tạo với đáy một góc bằng 60 0 . (P) cắt khối trụ theo thiết diện là một phần của elip. Diện tích thiết diện đó bằng
A. 4 π 3 - 3 2 R 2
B. 2 π 3 - 3 4 R 2
C. 2 π 3 + 3 4 R 2
D. 4 π 3 + 3 2 R 2
Cho hình trụ có các đáy là hai hình tròn tâm O và O’, bán kính đáy bằng a, chiều cao bằng
a
2
. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn đáy tâm O’ lấy điểm O sao cho AB 2a. Tính thể tích của khối tứ diện OO′B′A. A.
a
3
3
2
B.
a
3...
Đọc tiếp
Cho hình trụ có các đáy là hai hình tròn tâm O và O’, bán kính đáy bằng a, chiều cao bằng a 2 . Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn đáy tâm O’ lấy điểm O' sao cho AB' = 2a. Tính thể tích của khối tứ diện OO′B′A.
A. a 3 3 2
B. a 3 2 12
C. a 3 2 6
D. a 3 6
Cho hình trụ T có trục OO Trên hai đường tròn đáy (O) và (O) lần lượt lấy hai điểm A và B sao cho AB a và đường thẳng AB tạo với đáy của hình trụ góc
60
°
Gọi hình chiếu của B trên mặt phẳng đáy chứa đường tròn (O) là B Biết rằng
A
O
B
^
120
°
Tính khoảng cách d giữa hai đường thẳng AB và OO A.
d
a...
Đọc tiếp
Cho hình trụ T có trục OO' Trên hai đường tròn đáy (O) và (O') lần lượt lấy hai điểm A và B sao cho AB = a và đường thẳng AB tạo với đáy của hình trụ góc 60 ° Gọi hình chiếu của B trên mặt phẳng đáy chứa đường tròn (O) là B' Biết rằng A O B ^ = 120 ° Tính khoảng cách d giữa hai đường thẳng AB và OO'

A. d = a 3 4
B. d = a 3 12
C. d = a 3 8
D. d = a 3 16
Cho hình trụ có chiều cao h a
3
, bán kính đáy r a. Gọi O,O’ lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm A, B sao cho hai dường thẳng AB và OO’ chéo nhau và góc giữa hai đường thẳng AB với OO’ bằng 300. Khoảng cách giữa hai đường thẳng AB và OO’ bằng : A.
a
6
B.
a
6...
Đọc tiếp
Cho hình trụ có chiều cao h = a 3 , bán kính đáy r = a. Gọi O,O’ lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm A, B sao cho hai dường thẳng AB và OO’ chéo nhau và góc giữa hai đường thẳng AB với OO’ bằng 300. Khoảng cách giữa hai đường thẳng AB và OO’ bằng :
A. a 6
B. a 6 2
C. a 3
D. a 3 2
Cho hình trụ có hai đáy là hai hình tròn (O) và (O), chiều cao bằng 2R và bán kính đáy R. mặt phẳng (P) đi qua trung điểm của (OO) và tạo với OO một góc
30
°
cắt đường tròn dáy theo dây cung . Tính độ dài day cung đó theo R A.
4
R
3
3
B.
2
R
6
3...
Đọc tiếp
Cho hình trụ có hai đáy là hai hình tròn (O) và (O'), chiều cao bằng 2R và bán kính đáy R. mặt phẳng (P) đi qua trung điểm của (OO') và tạo với OO' một góc 30 ° cắt đường tròn dáy theo dây cung . Tính độ dài day cung đó theo R
A. 4 R 3 3
B. 2 R 6 3
C. 2 R 3
D. 2 R 3 3