Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật. Một mặt phẳng thay đổi nhưng luôn song song với đáy và cắt các cạnh bên SA, SB, SC, SD lần lượt tại M, N, P, Q. Gọi M' , N', P', Q lần lượt là hình chiếu vuông góc của M, N, P, Q lên mặt phẳng (ABCD) Tính tỉ số S M S A để thể tích khối đa diện M N P Q . M ' N ' P ' Q ' đạt giá trị lớn nh
A. 2/3
B. 1/2
C. 1/3
D. 3/4
Đáp án A
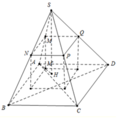
Ta có: S M S A = x = M N A B ⇒ M N = x . A B
Tương tự M Q = x A D
M M ' S H = A M S A = 1 − x ⇒ M M ' = 1 − x S H
Do đó V M N P Q . M ' N ' P ' Q ' = x 2 1 − x . A B . A D . S H .
Xét hàm số f x = x 2 1 − x = x 2 − x 3 ⇒ f ' x = 2 x − 3 x 2
Do đó f ' x = 0 ⇔ x = 2 3 .
Vậy V M N P Q . M ' N ' P ' Q ' = x 2 1 − x . A B . A D . S H lớn nhất khi S M S A = 2 3 .



