Đáp án A
Phương pháp:
Sử dụng tỉ số thể tích: Cho các điểm M, N, P lần lượt thuộc các cạnh SA, SB, SC của hình chóp SABC. Khi đó ta có: V S M N P V S A B C = S M S A . S N S B . S P S C
Cách giải:
Áp dụng tỉ số thể tích ta có:
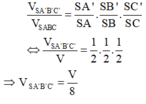
Đáp án A
Phương pháp:
Sử dụng tỉ số thể tích: Cho các điểm M, N, P lần lượt thuộc các cạnh SA, SB, SC của hình chóp SABC. Khi đó ta có: V S M N P V S A B C = S M S A . S N S B . S P S C
Cách giải:
Áp dụng tỉ số thể tích ta có:
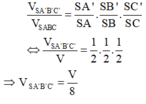
Cho khối chóp S . A B C , trên ba cạnh S A , S B , S C lần lượt lấy ba điểm A ' , B ' , C ' sao cho S A ' = 2 3 A A ' , S B ' = 1 4 S B , S C ' = 1 2 C C ' . Gọi V và V′ lần lượt là thể tích của các khối chóp S . A B C và S . A ' B ' C ' . Khi đó tỉ số V ' V là
A. 1 30
B. 1 24
C. 1 8
D. 1 8
Cho khối chóp S.ABC, trên ba cạnh SA, SB, SC lần lượt lấy ba điểm A ' , B ' , C ' sao cho S A ' = 1 3 S A , S B ' = 1 3 S B , S C ' = 1 3 S C . Gọi V và V' lần lượt là thể tích của các khối chóp S.ABC và S.A'B'C'. Khi đó tỉ số V ' V là
A. 1 6
B. 1 3
C. 1 27
D. 1 9
Khối chóp chóp tam giác S.ABC có thể tích V. Gọi M,N,P lần lượt là trung điểm các cạnh SA, SB, SC. Thể tích của khối đa diện ABCMNP bằng
A. V 8
B. 3 V 4
C. 7 V 8
D. V 4
Cho hình chóp tứ giác S . A B C D có thể tích bằng V. Lấy điểm A’ trên cạnh SA sao cho S A ' = 1 3 S A . Một mặt phẳng qua A’ và song song với đáy của hình chóp cắt các cạnh S B , S C , S D lần lượt tại B ' , C ' , D ' . Khi đó thể tích của khối chóp S . A ' B ' C ' D ' tính theo a bằng
A. V 3
B. V 9
C. V 27
D. V 81
Cho hình chóp tứ giác S.ABCD đáy là hình bình hành có thể tích bằng V. Lấy điểm B', D' lần lượt là trung điểm của các cạnh SB và SD. Mặt phẳng (AB'D') cắt cạnh SC tại C'. Khi đó thể tích khối chóp S.AB'C'D' bằng
A. V 3
B. 2 V 3
C. V 3 3
D. V 6
Cho khối chóp S.ABC trên ba cạnh SA,SB,SC lần lượt lấy ba điểm A', B', C' sao cho S A ' = 1 2 S A ; S B ' = 1 3 S B ; S C ' = 1 4 S C , Gọi V và V' lần lượt là thể tích của khối chóp S.ABC và S.A'B'C' Khi đó tỉ số V ' V là:
A.12
B. 1 12
C.24
D. 1 24
Cho khối chóp S.ABC có thể tích bằng 16 c m 3 . Gọi M, N, P lần lượt là trung điểm của các cạnh SA, SB, SC. Tính thể tích V của khối tứ diện AMNP.
A. V = 8 c m 3 .
B. V = 14 c m 3 .
C. V = 12 c m 3 .
D. V = 2 c m 3 .
Cho hình chóp tứ giác S.ABCD có thể tích bằng V. Lấy điểm A ' trên cạnh SA sao cho S A ' = 1 3 S A . Mặt phẳng qua A ' và song song với đáy của hình chóp cắt các cạnh SB, SC, SD lần lượt tại B ' C ' D ' . Tính theo V thể tích khối chóp S.A’B’C’D’ ?
A. V 3
B. V 81
C. V 27
D. V 9
Cho hình chóp S.ABC, trên cạnh SA, SB, SC lần lượt lấy ba điểm A', B', C' sao cho S A = 2 S A ' ; S B = 3 S B ' và S C = 4 S C ' . Gọi V' và V lần lượt là thể tích của khối chóp S.A'B'C' và S.ABC. Khi đó tỉ số V ' V bằng bao nhiêu?
A. 1 6
B. 1 12
C. 1 24
D. 1 9