Xét hai tam giác vuông ADI và CDL có:
AD = CD (cạnh hình vuông)
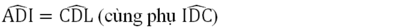
Nên ΔADI = ΔCDL (cạnh góc cuông và góc nhọn)
Suy ra DI = DL hay ΔDIL cân. (đpcm)
Xét hai tam giác vuông ADI và CDL có:
AD = CD (cạnh hình vuông)
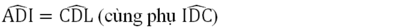
Nên ΔADI = ΔCDL (cạnh góc cuông và góc nhọn)
Suy ra DI = DL hay ΔDIL cân. (đpcm)
Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:
a) Tam giác DIL là một tam giác cân
b) Tổng
1 DI 2 + 1 DK 2
không đổi khi I thay đổi trên cạnh AB.
Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia Cb cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt BC tại L. Chứng minh rằng:
a) Tam giac DIL là một tam giác cân;
b) tổng 1/DI2 +1/DK2 không đổi khi I thay đổi trên cạnh AB.
Cho hình vuông ABCD . Gọi I là một điểm nằm giữa A và B.Tia DI và tia CB cắt nhau ở K . Kẻ đường thẳng qua D , vuông góc với DI .Đường thẳng này cắt đường thẳng BC tại L.Chứng minh rằng:
a) Tam giác DIL là một tam giác cân;
b) Tổng 1/DI2+1/DK2 không thay đổi khi I thay đổi trên cạnh AB.
cho hình vuông ABCD. Gọi I là một điểm nằm giữa AB. Tia DI và CB cắt nhau tại K, kẻ đường thẳng qua , vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. C/M
a) Tam giác DIL cân
b) Tổng 1/DI2 + 1/DK2 không đổi khi I thay đổi trên AB
Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thằng này cắt đường thẳng BC tại L. Tìm vị trí điểm I trên cạnh AB sao cho diện tích tam giác DKL bé nhất.
Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:
Tổng 1 D I 2 + 1 D K 2 không đổi khi I thay đổi trên cạnh AB.
Cho hình vuông ABCD. Gọi E là một điểm nằm giữa A, B. Tia DE và tia CB cắt nhau ở F. Kẻ đường thẳng qua D và vuông góc với DE, đường thẳng này cắt đường thẳng BC tại K. Chứng minh rằng:
a) Tam giác DEK vuông cân tại D
b) \(\dfrac{1}{DE^2}+\dfrac{1}{DF^2}\) không đổi khi E chuyển động trên AB.
Câu 9: Cho hình vuông ABCD . Gọi E là một điểm nằm giữa A, B . Tia DE và tia CB cắt nhau ở F . Kẻ đường thẳng qua D vuông góc với DE , đường thẳng này cắt đường thẳng BC tại G . Chứng minh rằng:
a) Tam giác DDEG cân.
Cho hình vuông ABCD.Gọi I là 1 điểm nằm giữa A và B.Tia DI và tia CB cắt nhau ở K.Kẻ đường thẳng qua D,vuông góc với DI.Đường thẳng này cắt CB tại L. C/m rằng: a) Tam Giác DIL là 1 tam giác cân b)Tổng 1DI21DI2 +1DK21DK2 không đổi Khi I thay đổi trên cạnh AB