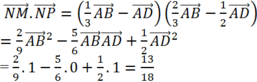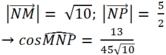Các câu hỏi tương tự
Cho tứ giác ABCD. Trên cạnh AB; CD lấy lần lượt các điểm M, N sao cho
3
A
M
→
2
A
B
→
và
3
D
N
→
2
D
C
→
.
Tính vectơ
M
N
→
theo hai ve...
Đọc tiếp
Cho tứ giác ABCD. Trên cạnh AB; CD lấy lần lượt các điểm M, N sao cho 3 A M → = 2 A B → và 3 D N → = 2 D C → . Tính vectơ M N → theo hai vectơ A D → , B C → .
A. M N → = 1 3 A D → + 1 3 B C → .
B. M N → = 1 3 A D → − 2 3 B C → .
C. M N → = 1 3 A D → + 2 3 B C → .
D. M N → = 2 3 A D → + 1 3 B C → .
Cho tứ giác ABCD. Trên cạnh AB; CD lấy lần lượt các điểm M; N sao cho
3
A
M
→
2
A
B
→
và
3
D
N
→
2
D
C
→
.
Tính vectơ
M
N
→
theo hai ve...
Đọc tiếp
Cho tứ giác ABCD. Trên cạnh AB; CD lấy lần lượt các điểm M; N sao cho 3 A M → = 2 A B → và 3 D N → = 2 D C → . Tính vectơ M N → theo hai vectơ A D → , B C → .
A. M N → = 1 3 A D → + 1 3 B C → .
B. M N → = 1 3 A D → − 2 3 B C → .
C. M N → = 1 3 A D → + 2 3 B C → .
D. M N → = 2 3 A D → + 1 3 B C → .
Cho hình bình hành ABCD, lấy M trên cạnh AB và N trên Cd sao cho AM=1/3AB, DN=1/3DC. gọi I và J thảo mãn BC=mBC, AI=nAI. Khi J là trọng tâm tam giác BMN thì tích m.n bằng mấy?
Tất cả là vecto đấy ạ
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD trên đoạn AC lấy M sao cho AC=4AM và N là trung điểm cạnh CD
CMR: Tam giác BMN là tam giác vuông cân
Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD. Gọi M là trung điểm cạnh BC, N là điểm trên cạnh CD sao cho CN 2ND. Giả sử M(, ) và đường thẳng AN có phương trình 2x – y – 3 0. Tìm tọa độ điểm A.
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD. Gọi M là trung điểm cạnh BC, N là điểm trên cạnh CD sao cho CN = 2ND. Giả sử M(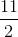 ,
,  ) và đường thẳng AN có phương trình 2x – y – 3 = 0. Tìm tọa độ điểm A.
) và đường thẳng AN có phương trình 2x – y – 3 = 0. Tìm tọa độ điểm A.
Cho hình vuông ABCD . gọi M,N,P,Q lần lượt là các điểm trên các cạnh AB , BC,CD,DA . Sao cho AM/AB=BN/BC=CP/CD=DQ/DA=1/3 . Chứng minh rằng vector MN=QP , MQ=NP
Xem chi tiết
trong mặt phẳng hệ tọa độ Oxy cho hình thang cân ABCD có hai đường chéo BD và AC vuông góc với nhau tại H và AD 2 BC. Gọi M là điểm nằm trên cạnh AB sao cho AB 3 AM N là trung điểm HC. biết B 1 3 đường thẳng HM đi qua T 2 3 đường thẳng DN có phương trình x 2y 2 0 . tìm tọa độ các điểm A,C,D
Cho tam giác đều ABC, độ dài cạnh là 3a . Lấy M, N, P lần lượt nằm trên các cạnh BC, CA, AB sao cho BM = a; CN = 2a và AP = x . Tính x để AM vuông góc với PN.
A. x = a
B. x = 2a
C. x = 0,8.a
D. x = 0,5.a
trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD. Điểm N3;2) là trung điểm cạnh BC, các điểm M(-2;2) và P(2-1) lần lượt nằm trên cạnh ABvaf DC sao cho AM=Cp. xác định tọa độ các đỉnh của hình chữ nhật AND