Gọi Q là trung điểm AD chứng mình MNPQ là hình bình hành ⇒ M, N, P, Q cùng thuộc một mặt phẳng ⇒ thiết diện là hình bình hành.
Gọi Q là trung điểm AD chứng mình MNPQ là hình bình hành ⇒ M, N, P, Q cùng thuộc một mặt phẳng ⇒ thiết diện là hình bình hành.

Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. G là trọng tâm của tam giác SAB. Thiết diện của hình chóp ![]() cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB, CD để thiết diện đó là hình bình hành?
cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB, CD để thiết diện đó là hình bình hành?

A. AB=3CD
B. AB=2CD
C. CD=2AB
D. CD=3AB
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB // CD. Gọi M, N lần lượt là trung điểm của AD và BC; gọi G là trọng tâm tam giác SAB. Thiết diện của hình chóp với mặt phẳng (MNG) là hình bình hành thì
A. AB = 3CD
B. AB = 2CD
C. CD = 3AB
D. CD = 2AB
Cho tứ diện ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh AB, AC sao cho A M A B = A N A C ; gọi I và J lần lượt là trung điểm của BD, CD. Tứ giác MNJI là hình gì. Tìm điều kiện để tứ giác MNJI là hình bình hành.
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành và M; N lần lượt là trung điểm của AB; CD . Xác định thiết diện của hình chóp cắt bởi (α) đi qua MN và song song với mặt phẳng (SAD).Thiết diện là hình gì?
A. tứ giác
B. hình thang
C. hình thang cân
D. hình bình hành
Cho tứ diện ABCD. Gọi M, N, P, Q, R và S lần lượt trung điểm của AB, CD, BC, AD, AC và BD. Chứng minh rằng tứ giác MNPQ là hình bình hành. Từ đó suy ra ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.
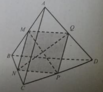
Cho hình tứ diện ABCD. Gọi M và N lần lượt là các trung điểm của AB và CD.
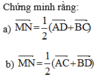
Bt2: cho hình chóp S.ABCD đáy là tứ giác lồi có AB>CD .gọi M,N lần lượt là trung điểm của cạnh SA và SD .a) tìm giao tuyến (SAB) và (SCD).b) tìm giao tuyến của (MNC) và (ABCD).c)tìm giao điểm của MN và (ABN).d) tìm thiết diện của hình chóp vs mp (BMN)
Cho hình chóp S.ABCD có đáy là hình thang ABCD (có đáy nhỏ BC). Gọi M, N lần lượt là trung điểm của AB và SD, O là giao điểm của AC và DM.
a) Tìm giao điểm của MN và mặt phẳng (SAC).
b) Tìm thiết diện của hình chóp với mặt phẳng (NBC). Thiết diện đó là hình gì?
Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm AC, BC, BD, AD. Tìm điều kiện để tứ giác MNPQ là hình thoi.
A. AB = BC.
B. BC = AD.
C. AC = BD.
D. AB = CD.