Các câu hỏi tương tự
Một hình trụ có bán kính r và chiều cao h r√3.a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.b) TÍnh thể tích khối trụ tạo nên bởi hình trụ đã cho.c) Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng AB và trục của hình trụ bằng 300. TÍnh khoảng cách giữa đường thẳng AB và trục của hình trụ
Đọc tiếp
Một hình trụ có bán kính r và chiều cao h = r√3.
a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.
b) TÍnh thể tích khối trụ tạo nên bởi hình trụ đã cho.
c) Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng AB và trục của hình trụ bằng 300. TÍnh khoảng cách giữa đường thẳng AB và trục của hình trụ
Cho hình trụ
T
có chiều cao bằng đường kính đáy, hai đáy là các hình tròn
O
;
r
và
O
;
r
. Gọi A là điểm di động trên đường tròn
O
;
r
v à B là điểm di động trên đường tròn
O
;
r...
Đọc tiếp
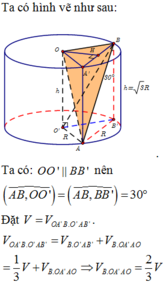
Cho hình trụ T có chiều cao bằng đường kính đáy, hai đáy là các hình tròn O ; r và O ' ; r . Gọi A là điểm di động trên đường tròn O ; r v à B là điểm di động trên đường tròn O ' ; r sao cho AB không là đường sinh của hình trụ T . Khi thể tích khối tứ diện O O ' A B đạt giá trị lớn nhất thì đoạn thẳng AB có độ dài bằng
A. 3 r
B. 2 + 2 r
C. 6 r
D. 5 r
Một hình trụ có bán kính đường tròn đáy là r và chiều cao
h
r
3
Lấy hai điểm A, B nằm trên đường tròn đáy của hình trụ sao cho góc giữa đường thẳng AB và hình trụ bằng
30
°
. Khi đó khoảng cách giữa đường thẳng AB với trục của hình trụ bằng A.
r
3
B.
r
3
2
C.
r...
Đọc tiếp
Một hình trụ có bán kính đường tròn đáy là r và chiều cao h = r 3 Lấy hai điểm A, B nằm trên đường tròn đáy của hình trụ sao cho góc giữa đường thẳng AB và hình trụ bằng 30 ° . Khi đó khoảng cách giữa đường thẳng AB với trục của hình trụ bằng
A. r 3
B. r 3 2
C. r 3 3
D. r 6 2
Cho hình trụ có chiều cao h 5, bán kính đáy r 2. Một đoạn thẳng có chiều dài bằng 6 và có hai đầu mút nằm trên hai đường tròn đáy. Tính khoảng cách d từ đoạn thẳng đó đến trục của hình trụ. A.
d
11
2
B. d 2 C.
d
5
2
D.
d
4
2
Đọc tiếp
Cho hình trụ có chiều cao h = 5, bán kính đáy r = 2. Một đoạn thẳng có chiều dài bằng 6 và có hai đầu mút nằm trên hai đường tròn đáy. Tính khoảng cách d từ đoạn thẳng đó đến trục của hình trụ.
A. d = 11 2
B. d = 2
C. d = 5 2
D. d = 4 2
Một hình trụ có bán kính bằng r và chiều cao
h
r
3
. Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa hai đường thẳng AB và trục của hình trụ bằng 30°. Tính khoảng cách giữa đường thẳng AB và trục của hình trụ. A.r B.
r
2
C.
r
3
2
D.
r
3
Đọc tiếp
Một hình trụ có bán kính bằng r và chiều cao h = r 3 . Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa hai đường thẳng AB và trục của hình trụ bằng 30°. Tính khoảng cách giữa đường thẳng AB và trục của hình trụ.
A.r
B. r 2
C. r 3 2
D. r 3
Cho khối trụ có hai đáy là hai hình tròn (O;R) và(O’;R),OO’4R. Trên đường tròn (O;R) lấy hai điểm A, B sao cho
A
B
R
3
. Mặt phẳng (P) đi qua A, B cắt đoạn OO’ và tạo với đáy một góc bằng 60 độ (P) cắt khối trụ theo thiết diện là một phần của hình elip. Diện tích thiết diện đó bằng A.
4
π
3
-...
Đọc tiếp
Cho khối trụ có hai đáy là hai hình tròn (O;R) và(O’;R),OO’=4R. Trên đường tròn (O;R) lấy hai điểm A, B sao cho A B = R 3 . Mặt phẳng (P) đi qua A, B cắt đoạn OO’ và tạo với đáy một góc bằng 60 độ (P) cắt khối trụ theo thiết diện là một phần của hình elip. Diện tích thiết diện đó bằng
A. 4 π 3 - 3 2 R 2
B. 2 π 3 - 3 4 R 2
C. 2 π 3 + 3 4 R 2
D. 4 π 3 + 3 2 R 2
Cho hình trụ có bán kính R và chiều cao
3
R
. Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục d của hình trụ bằng
30
°
. Tính khoảng cách giữa AB và trục của hình trụ. A.
d
A
B
,
d
R
3
2
B.
d...
Đọc tiếp
Cho hình trụ có bán kính R và chiều cao 3 R . Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục d của hình trụ bằng 30 ° . Tính khoảng cách giữa AB và trục của hình trụ.
A. d A B , d = R 3 2
B. d A B , d = R
C. d A B , d = R 3
D. d A B , d = R 2
Cho hình trụ có hai đáy là hai hình tròn (O; R) và (O; R). AB là một dây cung của đường tròn (O; R) sao cho tam giác OAB là tam giác đều và mặt phẳng (OAB) tạo với mặt phẳng chứa đường tròn (O;R) một góc 60 độ. Tính theo R thể tích V của khối trụ đã cho. A.
V
π
7
R
3
7
B.
V...
Đọc tiếp
Cho hình trụ có hai đáy là hai hình tròn (O; R) và (O'; R). AB là một dây cung của đường tròn (O; R) sao cho tam giác O'AB là tam giác đều và mặt phẳng (O'AB) tạo với mặt phẳng chứa đường tròn (O;R) một góc 60 độ. Tính theo R thể tích V của khối trụ đã cho.
A. V = π 7 R 3 7
B. V = 3 π 5 R 3 5
C. V = π 5 R 3 5
D. V = 3 π 7 R 3 7
Cho hình trụ tròn xoay có hai đáy là hai hình tròn (O;R),(O′;R). Biết rằng tồn tại dây cung AB của đường tròn O sao cho O′AB là tam giác đều và (O′AB) hợp với đường tròn O một góc
60
o
.
Tính diện tích xung quanh của hình trụ. A.
π
7
R
2
7
B.
4...
Đọc tiếp
Cho hình trụ tròn xoay có hai đáy là hai hình tròn (O;R),(O′;R). Biết rằng tồn tại dây cung AB của đường tròn O sao cho O′AB là tam giác đều và (O′AB) hợp với đường tròn O một góc 60 o . Tính diện tích xung quanh của hình trụ.
A. π 7 R 2 7
B. 4 π 7 R 2 7
C. 2 π 7 R 2 7
D. 6 π 7 R 2 7