Đáp án C.
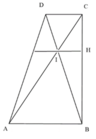
Phần thể tích chung của 2 hình nón T1 và T2 là 2 hính nón tạo bởi việc quay 2 tam giác HIB và HIC quanh BC.
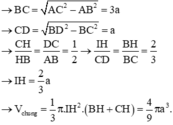
Đáp án C.

Phần thể tích chung của 2 hình nón T1 và T2 là 2 hính nón tạo bởi việc quay 2 tam giác HIB và HIC quanh BC.
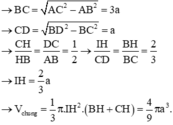
Trong không gian cho ABCD là hình chữ nhật, AB=2, AD=1. Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết d ( A B , d ) < d ( C D , d ) . Tính a biết rằng thể tích khối T gấp 3 lần thể tích của khối cầu có đường kính AB.
A. a = 3
B. a = - 1 + 2
C. a = 1 2
D. a = 15 2
Cho hình phẳng (D) được giới hạn bởi các đường x = 0 , x = π , y = 0 và y = − sin x . Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức:
A. V = π ∫ 0 π sin x d x .
B. V = π ∫ 0 π sin 2 x d x .
C. V = π ∫ 0 π − sin x d x .
D. V = ∫ 0 π sin 2 x d x .
Cho hình phẳng (D) giới hạn bởi các đường: y = x - π ; y = sinx ; x = 0 . Gọi V là thể tích khối tròn xoay tạo thành do (D) quay quanh trục hoành và V = p π 4 p ∈ ℚ . Giá trị của 24p bằng:
A. 8
B. 4
C. 24
D. 12
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y =sinx.cosx, trục tung, trục hoành và đường thẳng x =π/2 . Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox.
A. V =π/16.
B. V = π 2 16
C. V = π 2 + π 16
D. V = π 2 4
Cho hình thang ABCD vuông A và B với A B = B C = A D 2 = a . Quay hình thang và miền trong của nó quanh đường thẳng chứa cạnh BC. Tính thể tích V của khối tròn xoay được tạo thành.
A. V = 4 πa 3 3
B. V = 5 πa 3 3
C. V = 7 πa 3 3
D. V = πa 3
Cho hình thang ABCD vuông tại A và B với A B = B C = A D 2 = a . Quay hình thang và miền trong của nó quanh đường thẳng chứa cạnh BC. Tính thể tích V của khối tròn xoay được tạo thành.
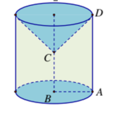
A. V = 4 π a 3 3
B. V = 5 π a 3 3
C. V = π a 3
D. V = 7 π a 3 3
Cho tam giác ABC vuông tại A, góc A B C ^ = 60 ∘ . Tính thể tích V của khối tròn xoay sinh bởi khi quay ∆ABC quanh trục AB, biết BC=2a.
A. V = π a 3
B. V = a 3
C. V = π a 3 3 3
D. V = 3 a 3
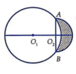
Cho hai đường tròn O 1 ; 5 và O 2 ; 3 cắt nhau tại hai điểm A, B sao cho AB là một đường kính của đường tròn O 2 . Gọi (D) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần gạch chéo như hình vẽ). Quay (D) quanh trục O 1 O 2 ta được một khối tròn xoay. Tính thể tích V của khối tròn xoay được tạo thành
A. V = 14 π 3
B. V = 68 π 3
C. V = 40 π 3
D. V = 36 π
Cho tứ diện ABCD có A D ⊥ A B C , ABC là tam giác vuông tại B. Biết B C = a , A B = a 3 , A D = 3 a . Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng
A. 3 3 π a 3 16
B. 8 3 π a 3 3
C. 5 3 π a 3 16
D. 4 3 π a 3 16