Question

Cho hình thang vuông ABCD ( Â = D̂ = 900 ), AB = 9cm; CD = 15cm; AC = 17cm. Tính độ dài các cạnh bên của hình thang.

Answer 1

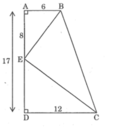
Áp dụng PTG: \(AD=\sqrt{AC^2-AD^2}=\sqrt{17^2-15^2}=8\left(cm\right)\)

Kẻ đg cao BH

Do đó \(\widehat{BAD}=\widehat{ADH}=\widehat{DHB}=90^0\) nên ABHD là hcn

Do đó \(AB=DH=9\left(cm\right);AD=BH=8\left(cm\right)\)

\(\Rightarrow HC=CD-DH=17-9=8\left(cm\right)\)

Áp dụng PTG cho tg BHC vuông tại H

\(BC=\sqrt{BH^2+CH^2}=\sqrt{64+64}=8\sqrt{2}\left(cm\right)\)

Vậy độ dài các cạnh bên AD,BC là 8 cm và \(8\sqrt{2}\) cm