Các câu hỏi tương tự
cho tam giác ABC vuông tại A đường phân giác BD từ d kẻ DH vuông góc với BCa, chứng minh rằng Δ BAD = Δ BHDb, chứng minh BD là đường trung trực của AHc, kéo dài tia HD và BA cắt nhau tại K so sánh KD và DH
Xem chi tiết
Tam giác ABC cân tại A có \(\widehat{BAC}=80^o\), trên hai cạnh BC, AC của tam giác lần lượt lấy hai điểm D, E sao cho \(\widehat{BAD}=50^o,\widehat{ABE}=30^o\). Tính số đo \(\widehat{BED}\).
Cho tam giác ABC nội tiếp (O;R) có ^B=3^C. Đường phân giác trong của góc A cắt BC tại D và cắt lại (O) tại M. Trên tia đối của tia MC, lấy điểm E sao cho ME=R. OE cắt AM tại S. Chứng minh S là tâm đường tròn ngoại tiếp tam giác ACE.
Cho tam giác ABC thỏa mãn \(\widehat{BAC}=2.\widehat{ABC}\), M là trung điểm cạnh AB. Đường thẳng qua B vuông góc với BC cắt đường thẳng AC tại E. Chứng minh rằng MA là phân giác của \(\widehat{CME}\).
cho tam giác ABC vuông tại A (ACAB) Đường cao AH (H thuộc BC) trên tia HC lấy điểm D sao cho HDHA . Đường vuông góc với BC tại D cắt AC tại E .a) CMR hai tam giác BEC và ADC đồng dạng .Tính độ dài BE theo mAB b) ọi M là tung điểm của đoạn BE . CMR ha tam giác BHM và BEC đồng dạng . Tính số đo góc AHM c) Tia AM cắt BC tại G cm dfrac{text{GB}}{text{BC}}dfrac{text{HD}}{text{AH+HC}}
Đọc tiếp
cho tam giác ABC vuông tại A (AC>AB) Đường cao AH (H thuộc BC) trên tia HC lấy điểm D sao cho HD=HA . Đường vuông góc với BC tại D cắt AC tại E .
a) CMR hai tam giác BEC và ADC đồng dạng .Tính độ dài BE theo m=AB
b) ọi M là tung điểm của đoạn BE . CMR ha tam giác BHM và BEC đồng dạng . Tính số đo góc AHM
c) Tia AM cắt BC tại G cm \(\dfrac{\text{GB}}{\text{BC}}=\dfrac{\text{HD}}{\text{AH+HC}}\)
Trong mặt phẳng với hệ trục Oxy, cho tam giác ABC vuông tại C, có phân giác AD với Dleft(dfrac{7}{2};-dfrac{7}{2}right) thuộc BC. Gọi E, F lần lượt thuộc các cạnh AB, AC sao cho AEAF. Đường thẳng EF cắt BC tại K. Biết Eleft(dfrac{3}{2};-dfrac{5}{2}right), F có hoành độ nhỏ hơn 3 và phương trình đường thẳng AK là x-2y-30. Viết phương trình các cạnh tam giác ABC.
Đọc tiếp
Trong mặt phẳng với hệ trục Oxy, cho tam giác ABC vuông tại C, có phân giác AD với \(D\left(\dfrac{7}{2};-\dfrac{7}{2}\right)\) thuộc BC. Gọi E, F lần lượt thuộc các cạnh AB, AC sao cho \(AE=AF\). Đường thẳng EF cắt BC tại K. Biết E\(\left(\dfrac{3}{2};-\dfrac{5}{2}\right)\), F có hoành độ nhỏ hơn 3 và phương trình đường thẳng \(AK\) là \(x-2y-3=0\). Viết phương trình các cạnh tam giác ABC.
Cho tam giác ABC với phân giác trong AD. Biết AB 5; BC 6; CA 7. Khi đó
A
D
→
bằng A. B. C. D.
Đọc tiếp
Cho tam giác ABC với phân giác trong AD. Biết AB= 5; BC= 6; CA= 7. Khi đó A D → bằng
A. 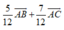
B. 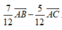
C. 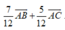
D. ![]()
Cho tam giác ABC vuông tại A biết BC =13, AC = 12. Đường phân giác trong của góc A cắt cạnh BC tại D. Tính AD
giúp mình với ạ
Bài 4 : ( 3,5 điểm)Cho tam giác ABC nhọn, vẽ đường tròn (O) đường kính BC cắt AB, AC lần lượt tại F và E. CF cắt BE tại H.a) Chứng minh tứ giác AEHF nội tiếpb) Gọi I là tâm đường tròn ngoại tiếp tứ giác AEHF, Tính số đo cung EHF, diện tích hình quạt IEHF của đường tròn (I) nếu góc BAC 60o, AH 4 cm.c) AH giao BC tại D. Chứng minh FH là tia phân giác của góc DFEd) Chứng minh 2 tiếp tuyến của (O) tại E, F và AH đồng quy tại 1 điểm
Đọc tiếp
Bài 4 : ( 3,5 điểm)Cho tam giác ABC nhọn, vẽ đường tròn (O) đường kính BC cắt AB, AC lần lượt tại F và E. CF cắt BE tại H.
a) Chứng minh tứ giác AEHF nội tiếp
b) Gọi I là tâm đường tròn ngoại tiếp tứ giác AEHF, Tính số đo cung EHF, diện tích hình quạt IEHF của đường tròn (I) nếu góc BAC = 60o, AH = 4 cm.
c) AH giao BC tại D. Chứng minh FH là tia phân giác của góc DFE
d) Chứng minh 2 tiếp tuyến của (O) tại E, F và AH đồng quy tại 1 điểm













