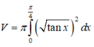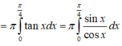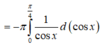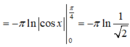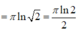Các câu hỏi tương tự
Cho hình phẳng giới hạn bởi các đường
y
tan
x
,
y
0
;
x
0
;
x
π
4
quay xung quanh trục Ox. Tính thể tích vật thể tròn xoay được sinh ra A.
π
ln
...
Đọc tiếp
Cho hình phẳng giới hạn bởi các đường y = tan x , y = 0 ; x = 0 ; x = π 4 quay xung quanh trục Ox. Tính thể tích vật thể tròn xoay được sinh ra
A. π ln 2 2
B. π ln 3 4
C. π 4
D. π ln 2
Cho hình phẳng (D) được giới hạn bởi các đường
x
0
,
x
π
,
y
0
và
y
−
sin
x
. Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức: A.
V
π
∫
0
π
sin...
Đọc tiếp
Cho hình phẳng (D) được giới hạn bởi các đường x = 0 , x = π , y = 0 và y = − sin x . Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức:
A. V = π ∫ 0 π sin x d x .
B. V = π ∫ 0 π sin 2 x d x .
C. V = π ∫ 0 π − sin x d x .
D. V = ∫ 0 π sin 2 x d x .
Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường thẳng
y
cos
x
,
y
0
,
x
0
,
x
π
quay quanh trục Ox. A.
π
3
B.
π
2
2
C.
π
2
D. ...
Đọc tiếp
Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường thẳng y = cos x , y = 0 , x = 0 , x = π quay quanh trục Ox.
A. π 3
B. π 2 2
C. π 2
D. π 2 3
Tính thể tích V của vật thể tròn xoay sinh ra khi cho hình phẳng giới hạn bởi các đường
y
1
x
,
y
0
,
x
1
,
x
a
,
a
1
quay xung quanh trục Ox. A.
V
1
−
1
a
B.
V...
Đọc tiếp
Tính thể tích V của vật thể tròn xoay sinh ra khi cho hình phẳng giới hạn bởi các đường y = 1 x , y = 0 , x = 1 , x = a , a > 1 quay xung quanh trục Ox.
A. V = 1 − 1 a
B. V = 1 − 1 a π
C. V = 1 + 1 a π
D. V = 1 + 1 a
Tính thể tích vật thể tròn xoay tạo bởi phép quay xung quanh trục Ox hình phẳng giới hạn bởi các đường
y
0
,
y
x
,
y
x
−
2
A.
8
π
3
B.
16
π
3
C. ...
Đọc tiếp
Tính thể tích vật thể tròn xoay tạo bởi phép quay xung quanh trục Ox hình phẳng giới hạn bởi các đường y = 0 , y = x , y = x − 2
A. 8 π 3
B. 16 π 3
C. 10 π
D. 8 π
Cho hình phẳng giới hạn bởi các đường
y
1
1
+
4
-
3
x
, y 0, x 0, x 1 quay xung quanh trục Ox. Tính thể tích khối tròn xoay A.
π
4
4
ln
3
2...
Đọc tiếp
Cho hình phẳng giới hạn bởi các đường y = 1 1 + 4 - 3 x , y = 0, x = 0, x = 1 quay xung quanh trục Ox. Tính thể tích khối tròn xoay
A. π 4 4 ln 3 2 - 1
B. π 4 6 ln 3 2 - 1
C. π 4 9 ln 3 2 - 1
D. π 4 6 ln 3 2 - 1
Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường y x/4,y 0,x 1,x 4 quay xung quanh trục Ox là A. 21/16 B. 21π/16 C. 15/16 D. 15π/16
Đọc tiếp
Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường y =x/4,y =0,x =1,x =4 quay xung quanh trục Ox là
A. 21/16
B. 21π/16
C. 15/16
D. 15π/16
Thể tích vật thể tròn xoay khi cho hình phẳng (H) giới hạn bởi các đường y xlnx; y 0 ; x 2 quay quanh trục Ox được tính bởi công thức nào? A.
π
∫
0
2
x
2
ln
2
xdx
B.
π
∫
1
2
x
2
ln
2
xdx
C. ...
Đọc tiếp
Thể tích vật thể tròn xoay khi cho hình phẳng (H) giới hạn bởi các đường y = xlnx; y = 0 ; x = 2 quay quanh trục Ox được tính bởi công thức nào?
A. π ∫ 0 2 x 2 ln 2 xdx
B. π ∫ 1 2 x 2 ln 2 xdx
C. ∫ 0 2 x 2 ln 2 xdx
D. ∫ 1 2 xlnxdx
Thể tích khối tròn xoay sinh ra bởi hình phẳng giới hạn bởi các đường
y
1
x
−
3
,
y
0
,
x
0
,
x
2
quay một vòng quanh...
Đọc tiếp
Thể tích khối tròn xoay sinh ra bởi hình phẳng giới hạn bởi các đường y = 1 x − 3 , y = 0 , x = 0 , x = 2 quay một vòng quanh trục Ox là (theo đơn vị thể tích)
A. 2 π
B. 2 3 π
C. 4 3 π
D. 1 3 π