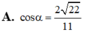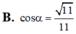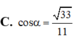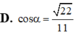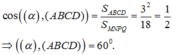Các câu hỏi tương tự
Cho tứ diện ABCD. Qua điểm M nằm trên AC ta dựng một mặt phẳng (α) song song với AB và CD. Mặt phẳng này lần lượt cắt các cạnh BC, BD và AD tại N, P và Q.
a) Tứ giác MNPQ là hình gì?
b) Gọi O là giao điểm hai đường chéo của tứ giác MNPQ. Tìm tập hợp các điểm O khi M di động trên đoạn AC.
Cho hình chóp S. ABCD. Gọi
A
1
là trung điểm của cạnh SA và
A
2
là trung điểm của đoạn
A
A
1
. Gọi (α) và (β) là hai mặt phẳng song song với mặt phẳng (ABCD) và lần lượt đi qua
A
1
,
A
2
. Mặt phẳng (α) cắt các cạnh SB, SC, SD lần lượt tại
B...
Đọc tiếp
Cho hình chóp S. ABCD. Gọi A 1 là trung điểm của cạnh SA và A 2 là trung điểm của đoạn A A 1 . Gọi (α) và (β) là hai mặt phẳng song song với mặt phẳng (ABCD) và lần lượt đi qua A 1 , A 2 . Mặt phẳng (α) cắt các cạnh SB, SC, SD lần lượt tại B 1 , C 1 , D 1 . Mặt phẳng (β) cắt các cạnh SB, SC, SD lần lượt tại B 2 , C 2 , D 2 . Chứng minh:
a) B 1 , C 1 , D 1 lần lượt là trung điểm của các cạnh SB, SC, SD.
b) B 1 B 2 = B 2 B , C 1 C 2 = C 2 C , D 1 D 2 = D 2 D .
c) Chỉ ra các hình chóp cụt có một đáy là tứ giác ABCD.
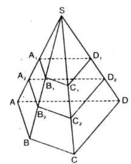
Cho hình hộp ABCD.ABCD Trên các cạnh AA’; BB’; CC’ lần lượt lấy ba điểm M, N, P sao cho Biết mặt phẳng (MNP) cắt cạnh DD’ tại Q. Tính tỉ số
D
Q
D
D
A.
1
6
B.
1
4
C.
3
8
D....
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' Trên các cạnh AA’; BB’; CC’ lần lượt lấy ba điểm M, N, P sao cho 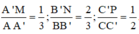 Biết mặt phẳng (MNP) cắt cạnh DD’ tại Q. Tính tỉ số
D
'
Q
D
D
'
Biết mặt phẳng (MNP) cắt cạnh DD’ tại Q. Tính tỉ số
D
'
Q
D
D
'
A. 1 6
B. 1 4
C. 3 8
D. 2 9
Cho hình hộp ABCD.A’B’C’D’. Trên các cạnh AA’, BB’, CC’ lần lượt lấy ba điểm M, N, P sao cho Biết mặt phẳng (MNP) cắt cạnh DD’ tại Q. Tính tỉ số
D
Q
D
D
A.
1
6
B.
1
3
C. ...
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’. Trên các cạnh AA’, BB’, CC’ lần lượt lấy ba điểm M, N, P sao cho 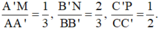 Biết mặt phẳng (MNP) cắt cạnh DD’ tại Q. Tính tỉ số
D
'
Q
D
D
'
Biết mặt phẳng (MNP) cắt cạnh DD’ tại Q. Tính tỉ số
D
'
Q
D
D
'
A. 1 6
B. 1 3
C. 5 6
D. 2 3
Cho hình hộp ABCD.ABCD. Gọi M và N lần lượt là trung điểm của hai cạnh bên AA và CC. Một điểm P nằm trên cạnh bên DD.a) Xác định giao điểm Q của đường thẳng BB với mặt phẳng (MNP).b) Mặt phẳng (MNP) cắt hình hộp theo một thiết diện. Thiết diện đó có tính chất gì?c) Tìm giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) của hình hộp.
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D'. Gọi M và N lần lượt là trung điểm của hai cạnh bên AA' và CC'. Một điểm P nằm trên cạnh bên DD'.
a) Xác định giao điểm Q của đường thẳng BB' với mặt phẳng (MNP).
b) Mặt phẳng (MNP) cắt hình hộp theo một thiết diện. Thiết diện đó có tính chất gì?
c) Tìm giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) của hình hộp.
Cho hình chóp đều S.ABCD có độ dài cạnh đáy bằng a. Gọi G là trọng tâm tam giác SAC. Mặt phẳng chứa AB và đi qua G cắt các cạnh, SC SD lần lượt tại M và N. Biết mặt bên của hình chóp tạo với đáy một góc bằng
60
0
. Thể tích khối chóp S. ABMN bằng
Đọc tiếp
Cho hình chóp đều S.ABCD có độ dài cạnh đáy bằng a. Gọi G là trọng tâm tam giác SAC. Mặt phẳng chứa AB và đi qua G cắt các cạnh, SC SD lần lượt tại M và N. Biết mặt bên của hình chóp tạo với đáy một góc bằng 60 0 . Thể tích khối chóp S. ABMN bằng
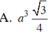
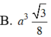
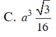
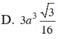
Cho hình lập phương ABCD.A BC D cạnh bằng a và K là một điểm nằm trên cạnh CC’ sao cho
C
K
2
a
3
. Mặt phẳng
(
α
)
qua A, K và song song với BD chia khối lập phương thành hai phần có...
Đọc tiếp
Cho hình lập phương ABCD.A' B'C' D' cạnh bằng a và K là một điểm nằm trên cạnh CC’ sao cho C K = 2 a 3 . Mặt phẳng ( α ) qua A, K và song song với BD chia khối lập phương thành hai phần có thể tích V 1 V 2 ( V 1 < V 2 ) . Tính tỉ số V 1 V 2
A. V 1 V 2 = 1 4
B. V 1 V 2 = 1 2
C. V 1 V 2 = 2 3
D. V 1 V 2 = 1 3
Hình chóp tứ giác đều S.ABCD có cạnh đáy có độ dài a. Mặt phẳng (P) qua A và vuông góc với SC cắt SB, SC, SD lần lượt tại B’, C’, D’ sao cho SB’ 2BB’. Tỉ số giữa thể tích hình chóp S.AB’C’D’ và thể tích hình chóp S.ABCD bằng A.
2
3
B.
4
9
C.
1
3
D.
4
27
Đọc tiếp
Hình chóp tứ giác đều S.ABCD có cạnh đáy có độ dài a. Mặt phẳng (P) qua A và vuông góc với SC cắt SB, SC, SD lần lượt tại B’, C’, D’ sao cho SB’= 2BB’. Tỉ số giữa thể tích hình chóp S.AB’C’D’ và thể tích hình chóp S.ABCD bằng
A. 2 3
B. 4 9
C. 1 3
D. 4 27
Cho hình lăng trụ ABC.ABC có đáy ABC là tam giác đều cạnh a; tam giác A’BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABC) M là trung điểm của cạnh CC’. Tính cosin góc
α
là góc giữa hai đường thẳng AA’ và BM
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a; tam giác A’BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABC) M là trung điểm của cạnh CC’. Tính cosin góc α là góc giữa hai đường thẳng AA’ và BM