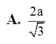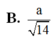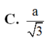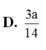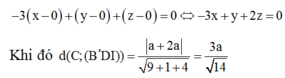Các câu hỏi tương tự
Cho hình lập phương ABCDABCDcó cạnh bằng a. Gọi M là điểm thuộc cạnh AB sao cho AM
1
3
A
B
. Tính khoảng cách h từ điểm C tới mặt phẳng (BDM).
Đọc tiếp
Cho hình lập phương ABCDA'B'C'D'có cạnh bằng a. Gọi M là điểm thuộc cạnh AB sao cho AM= 1 3 A B . Tính khoảng cách h từ điểm C tới mặt phẳng (B'DM).

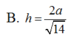
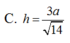
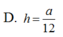
Cho hình lập phương ABCDABCD có cạnh bằng
α
Gọi M là điểm thuộc cạnh AB sao cho
A
M
1
3
A
B
Khoảng cách từ điểm C tới mặt phẳng (BDM) bằng
Đọc tiếp
Cho hình lập phương ABCDA'B'C'D' có cạnh bằng α Gọi M là điểm thuộc cạnh AB sao cho A M = 1 3 A B Khoảng cách từ điểm C tới mặt phẳng (B'DM) bằng
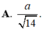
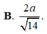
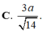
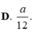
Trong không gian Oxyz, cho hình lập phương ABCD.ABCD có tọa độ A(1;2;1), C(3;6;-3). Gọi M là một điểm bất kỳ thuộc mặt cầu
(
S
)
:
x
-
2
2
+
y
-
4
2...
Đọc tiếp
Trong không gian Oxyz, cho hình lập phương ABCD.A'B'C'D' có tọa độ A(1;2;1), C(3;6;-3). Gọi M là một điểm bất kỳ thuộc mặt cầu ( S ) : x - 2 2 + y - 4 2 + z + 1 2 = 1 . Tính tổng các khoảng cách từ điểm M đến tất cả các mặt của hình lập phương ABCD.A'B'C'D'.
A. 2 3
B. 3 3
C. 6 3
D. 12
Giải bài toán sau đây bằng phương pháp tọa độ. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Tính khoảng cách từ đỉnh A đến các mặt phẳng (A'BD) và (B'D'C).
Cho khối chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và khoảng cách từ A đến mặt phẳng (SBC) bằng
a
2
2
. Gọi M là điểm thuộc cạnh SD sao cho SM2MD. Mặt phẳng (ABM) cắt cạnh SC tại điểm N. Thể tích khối đa diện MNABCD bằng
Đọc tiếp
Cho khối chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và khoảng cách từ A đến mặt phẳng (SBC) bằng a 2 2 . Gọi M là điểm thuộc cạnh SD sao cho SM=2MD. Mặt phẳng (ABM) cắt cạnh SC tại điểm N. Thể tích khối đa diện MNABCD bằng
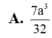
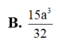
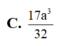
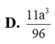
Cho lăng trụ
A
B
C
D
.
A
B
C
D
có đáy là hình vuông cạnh
a
3
. Hình chiếu vuông góc của điểm A lên mặt phẳng
(
A
B
C
D
)
trùng với tâm O của hình vuông
A
B
C
D
. Biết rằng...
Đọc tiếp
Cho lăng trụ A B C D . A ' B ' C ' D ' có đáy là hình vuông cạnh a 3 . Hình chiếu vuông góc của điểm A lên mặt phẳng ( A ' B ' C ' D ' ) trùng với tâm O của hình vuông A ' B ' C ' D ' . Biết rằng khoảng cách từ trọng tâm G của tam giác AB’D’ đến mặt phẳng (AA’D) bằng a 2 . Khoảng cách từ điểm O đến mặt phẳng ( A D C ' B ' ) bằng
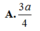

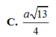
![]()
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi K là trung điểm của DD'. Tính khoảng cách giữa hai đường thẳng CK, A'D.
A. a
B. 3 a 8
C. 2 a 5
D. a 3
Cho hình lập phương ABCD.ABCD cạnh 2a, gọi M là trung điểm của BB và P thuộc cạnh sao cho
D
P
1
4
D
D
. Mặt phẳng (AMP) cắt CC tại N. Thể tích khối đa diện AMNPBCD bằng
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh 2a, gọi M là trung điểm của BB' và P thuộc cạnh sao cho D P = 1 4 D D ' . Mặt phẳng (AMP) cắt CC' tại N. Thể tích khối đa diện AMNPBCD bằng

![]()
![]()
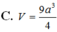

Cho hình lập phương ABCD.ABCD cạnh bằng a. Gọi K là trung điểm DD. Tính khoảng cách giữa hai đường thẳng CK và AD. A. 4a/3 B. a/3 C. 2a/3 D. 3a/4
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi K là trung điểm DD'. Tính khoảng cách giữa hai đường thẳng CK và A'D.
A. 4a/3
B. a/3
C. 2a/3
D. 3a/4