Đáp án A
Khoảng cách giữa đường chéo chính và đường chéo của một mặt bất kì trong hình lập phương cạnh a luôn bằng a 6 (hai đường chéo đó là hai đường thẳng chéo nhau).
Đáp án A
Khoảng cách giữa đường chéo chính và đường chéo của một mặt bất kì trong hình lập phương cạnh a luôn bằng a 6 (hai đường chéo đó là hai đường thẳng chéo nhau).
Bài 1. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 4. a. Tính độ dài đường chéo của hình lập phương. b. Tính góc giữa AC' và mặt đáy c. Tính góc giữa AC và B'C' d. Tính khoảng cách từ A đến (A'BD)
Cho hình lập phương ABCD.A'B'C'D'. Gọi (H) là hình cầu nội tiếp hình lập phương đó. Khi đó:
V H V ABCD . A ' B ' C ' D '
A. π /6 B. π /4
C. π /3 D. π /( 3 )
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Tính khoảng cách giữa hai đường thẳng AB' và CD'
A. 2 a 2
B. a
C. 2 a
D. 2a
Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi tâm O, cạnh a, B'D' = a 2 . Góc giữa CC' và mặt đáy là 60 0 , trung điểm H của AO là hình chiếu vuông góc của A' lên (ABCD). Thể tích của hình hộp là:
A. 3 a 3 8
B. a 3 3 8
C. 3 a 3 4
D. a 3 8
Cho hình lập phương ABCD.A'B'C'D'. Gọi (H) là hình trụ tròn xoay ngoại tiếp hình lập phương đó. Khi đó: V H V ABCD . A ' B ' C ' D '
A. 3/2 B. π /2
C. π /3 D. π /( 3 )
Cho hình lập phương ABCD.A'B'C'D'. Gọi (H) là hình nón tròn xoay nội tiếp hình lập phương đó. Khi đó: V H V ABCD . A ' B ' C ' D '
A. 1/3 B. π /6
C. π /8 D. π /12
Cho hình lập phương ABCDA'B'C'D'có cạnh bằng a. Gọi M là điểm thuộc cạnh AB sao cho AM= 1 3 A B . Tính khoảng cách h từ điểm C tới mặt phẳng (B'DM).

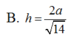
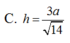
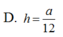
Cho khối lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi E và F lần lượt là trung điểm của B'C' và C'D'. Mặt phẳng (AEF) chia khối lập phương đó thành hai khối đa diện (H) và (H') trong đó (H) là khối đa diện chứa đỉnh A'. Tính thể tích của (H).
Cho tứ diện đều ABCD cạnh a. Tính khoảng cách h giữa AB và CD.
A. h = a 2 2
B. h = a 2
C. h = a 2 3
D. h = a 3 2