Đáp án A
Gọi M, N lần lượt là trung điểm AB, CD => MN = d(AB,CD).
Đáp án A
Gọi M, N lần lượt là trung điểm AB, CD => MN = d(AB,CD).
Tứ diện ABCD có AB, BC, CD đôi một vuông góc với AB = BC = CD = a. Tính khoảng cách h giữa BC và AD
A. h = a 3 3
B. h = a 2 2
C. h = a 3 2
D. h = a 2 3
Cho tứ diện đều ABCD cạnh a, tính khoảng cách giữa hai đường thẳng AB và CD.
A. a 2 2
B. a 3 2
C. a 3 3
D. a
Cho tứ diện đều ABCD cạnh a, tính khoảng cách giữa hai đường thẳng AB và CD.
A. a 2 2
B. a 3 2
C. a 3 3
D. a
Cho tứ diện đều ABCD có cạnh a. Tính khoảng cách giữa hai đường thẳng AB và CD.
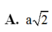
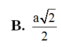
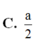
![]()
Cho hình chóp S.ABCD có SA ⊥ (ABCD); ABCD là hình vuông. Biết SA = a, AB = a 2 . Tính khoảng cách h giữa BD,SC
A. h = a 3 4
B. h = a 2 4
C. h = a 5
D. h = 2 a 5
Cho d 1 , d 2 chéo nhau và khoảng cách d 1 , d 2 = 3 . Biết d 1 ∥ v 1 → = 2 ; - 1 ; 1 ; d 1 ∥ v 2 → = 1 ; 1 ; 2 ; A , B ∈ d 1 và C , D ∈ d 2 sao cho A B = C D = 2 . Biết tứ diện ABCD có thể tích V không phụ thuộc việc chọn các điểm A, B, C, D. Tính V.
![]()
![]()
![]()
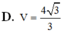
Trong không gian Oxyz, cho tứ diện đều ABCD có A(0;1;2). Gọi H là hình chiếu vuông góc của A lên mặt phẳng (BCD). Cho H(4;-3;-2). Tọa độ tâm I và bán kính R của mặt cầu (S) ngoại tiếp tứ diện ABCD là:
A. I(2; -1; 0); R = 2 3
B. I(4; -3; -2); R = 4 3
C. I(3; -2; -1); R = 3 3
D. I(3; -2; -1); R = 9
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Tính khoảng cách từ h giữa BD và SC.
A. h = a 2
B. h = a 2 4
C. h = a 3 4
D. h = a 2 3
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Khoảng cách giữa hai đường thẳng AB và CD là:
A. a 2 2
B. a 3 2
C. a 3 2
D. a