Chọn D.
Gọi 2a là cạnh của hình lập phương ta có hình nón tròn xoay nội tiếp hình lập phương đó có bán kính đáy r = a và chiều cao h = 2a
Suy ra:
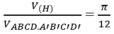
Chọn D.
Gọi 2a là cạnh của hình lập phương ta có hình nón tròn xoay nội tiếp hình lập phương đó có bán kính đáy r = a và chiều cao h = 2a
Suy ra:
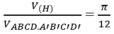
Cho hình lập phương ABCD.A'B'C'D'. Gọi (H) là hình trụ tròn xoay ngoại tiếp hình lập phương đó. Khi đó: V H V ABCD . A ' B ' C ' D '
A. 3/2 B. π /2
C. π /3 D. π /( 3 )
Cho hình lập phương ABCD.A'B'C'D'. Gọi (H) là hình cầu nội tiếp hình lập phương đó. Khi đó:
V H V ABCD . A ' B ' C ' D '
A. π /6 B. π /4
C. π /3 D. π /( 3 )
Cho hình lập phương có cạnh bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S 1 là diện tích 6 mặt của hình lập phương, S 2 là diện tích xung quanh của hình trụ. Tỉ số S 2 / S 1 bằng:
A. π /6 B. 1/2
C. π /2 D. π
Một hình nón có đường kính đáy là 2a π 3, góc ở đỉnh 120 ° . Thể tích của khối nón đó theo a là:
A. 2 3 π a 3 B. 3 π a 3
C. π a 3 D. π a 3 3
Quay hình phẳng Q giới hạn bởi các đường: y 1 = sinx và y 2 = 2x/ π quanh trục Ox, ta được một khối tròn xoay. Khi đó, thể tích khối tròn xoay này bằng:
A. 1/6 B. π /6
C. 8 D. π 2 /6
Quay hình phẳng Q giới hạn bởi các đường: y 1 = sinx và y 2 = 2x/π quanh trục Ox, ta được một khối tròn xoay. Khi đó, thể tích khối tròn xoay này bằng:
A. 1/6 B. π/6
C. 8 D. π 2 /6
Quay hình phẳng G giới hạn bởi các đường: y = x 3 ; y = 1, x = 0 xung quanh trục Oy. Khi đó thể tích của khối tròn xoay này bằng:
A. π B. 5 π /3
C. 3 π /5 D. 3/5
Cho hình lập phương ABCD.A'B'C'D' có cạnh a. Một khối nón có đỉnh là tâm của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuông A'B'C'D'. Kết quả tính diện tích toàn phần của khối nón có dạng bằng π a 2 4 ( b + c ) với b, c là hai số nguyên dương và b > 1 . Tính b.c.

![]()
![]()
![]()
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Một hình nón có đỉnh là tâm của hình vuông ABCD và có đường tròn đáy ngoại tiếp hình vuông A'B'C'D'. Diện tích xung quanh của hình nón đó là:
A. πa 3 2 3
B. πa 2 2 2
C. πa 3 2 2
D. πa 6 2 2