Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, cho ba điểm
A
-
2
;
1
;
0
,
B
4
;
4
;
-
3
,
C
2
;
3
;
-
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A - 2 ; 1 ; 0 , B 4 ; 4 ; - 3 , C 2 ; 3 ; - 2 và đường thẳng d : x - 1 1 = y - 1 - 2 = z - 1 - 1 . Gọi α là mặt phẳng chứa d sao cho A, B, C ở cùng phía đối với mặt phẳng α . Gọi d 1 , d 2 , d 3 lần lượt là khoảng cách từ A, B, C đến α . Tìm giá trị lớn nhất của T = d 1 + 2 d 2 + 3 d 3 .
A. T m a x = 2 21
B. T m a x = 6 14
C. T m a x = 14 + 203 3 + 3 21
D. T m a x = 203
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, cạnh SAa và vuông góc với mặt đáy. Gọi M, N lần lượt là trung điểm các cạnh BC, SD,
α
là góc giữa đường thẳng MN và
S
A
C
. Giá trị
tan
α
là A.
6
3
B.
6
2
C. ...
Đọc tiếp
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, cạnh SA=a và vuông góc với mặt đáy. Gọi M, N lần lượt là trung điểm các cạnh BC, SD, α là góc giữa đường thẳng MN và S A C . Giá trị tan α là
A. 6 3
B. 6 2
C. 3 2
D. 2 3
Cho lăng trụ ABC.A’B’C’có AB 2a, BC 2a, góc A’B’C’
120
0
. Hình chiếu vuông góc của A trên mặt phẳng (A’B’C’) trung với điểm của A’B’. Góc giữa đường thẳng AC’ và mặt phẳng (A’B’C’) bằng
60
0
. Gọi α là góc giữa hai mặt phẳng (BCC’B’) và (ABC). Khi đó, tan α có giá trị là: A.
21
B.
2...
Đọc tiếp
Cho lăng trụ ABC.A’B’C’có AB = 2a, BC = 2a, góc A’B’C’ = 120 0 . Hình chiếu vuông góc của A trên mặt phẳng (A’B’C’) trung với điểm của A’B’. Góc giữa đường thẳng AC’ và mặt phẳng (A’B’C’) bằng 60 0 . Gọi α là góc giữa hai mặt phẳng (BCC’B’) và (ABC). Khi đó, tan α có giá trị là:
A. 21
B. 2 2
C. 21 2
D. 2 21
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với
A
B
a
,
B
C
a
3
,
cạnh
S
A
2
a
,
S
A
⊥
A
B
C
D
.
Gọi
α
là góc giữa đường thẳng SC với mặt phẳng (ABCD). Giá trị tan bằng A. 2 B. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với A B = a , B C = a 3 , cạnh S A = 2 a , S A ⊥ A B C D . Gọi α là góc giữa đường thẳng SC với mặt phẳng (ABCD). Giá trị tan bằng
A. 2
B. 2
C. 1
D. 1 2
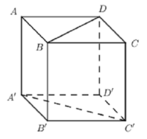
Cho hình lập phương ABCD.A′B′C′D′ có độ dài cạnh bằng 3. Một mặt phẳng (α) đồng thời cắt các cạnh AA′,BB′,CC′,DD′ lần lượt tại các điểm M,N,P,Q. Diện tích tứ giác MNPQ bằng 18. Góc giữa (α) và mặt phẳng đáy bằng A.
45
°
B.
30
°
C.
60
°
D.
0
°
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ có độ dài cạnh bằng 3. Một mặt phẳng (α) đồng thời cắt các cạnh AA′,BB′,CC′,DD′ lần lượt tại các điểm M,N,P,Q. Diện tích tứ giác MNPQ bằng 18. Góc giữa (α) và mặt phẳng đáy bằng
A. 45 °
B. 30 °
C. 60 °
D. 0 °
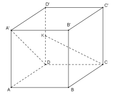
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 1. Gọi K là trung điểm của DD′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng CK và A′D bằng A.
10
5
B.
4
5
C.
10
10
D.
2
5
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 1. Gọi K là trung điểm của DD′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng CK và A′D bằng
A. 10 5
B. 4 5
C. 10 10
D. 2 5
Trong không gian Oxyz, cho mặt phẳng
α
:
2
x
+
3
y
-
2
z
+
12
0
. Gọi A, B, C lần lượt là giao điểm của
α
với 3 trục tọa độ, đường thẳng d đi qua tâm đường tròn ngoại tiếp tam giác ABC và vuông góc với
α
có phương trình là A.
x
+
3...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng α : 2 x + 3 y - 2 z + 12 = 0 . Gọi A, B, C lần lượt là giao điểm của α với 3 trục tọa độ, đường thẳng d đi qua tâm đường tròn ngoại tiếp tam giác ABC và vuông góc với α có phương trình là
A. x + 3 2 = y + 2 3 = z - 3 - 2
B. x + 3 2 = y - 2 - 3 = z - 3 2
C. x + 3 2 = y - 2 3 = z - 3 - 2
D. x - 3 2 = y - 2 3 = z + 3 - 2
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
, biết
A
C
3
,
C
D
2,
D
A
5
. Góc giữa hai mặt phẳng...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' , biết A C = 3 , C D ' = 2, D ' A = 5 . Góc giữa hai mặt phẳng A C D ' và A ' B ' C ' D ' là α, tan α bằng
A. 3 2 2
B. 2 6 3
C. 2 3
D. 30 6
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của các cạnh BC và SA,
α
là góc tạo bởi đường thẳng EM và mặt phẳng
S
B
D
,
tan
α
bằng A.
2
B.
3
C. 2 D. 1
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của các cạnh BC và SA, α là góc tạo bởi đường thẳng EM và mặt phẳng S B D , tan α bằng
A. 2
B. 3
C. 2
D. 1