Dùng phương pháp tọa độ hóa.
Đặt hệ trục tọa độ, ở đây như thầy đã trình bày ta nên chọn gốc tại P trục Ox, Oy là PA và PC.
Gọi α góc tạo bởi hai mặt phẳng ( AB'C' ) và (MNP)
Khi đó cos α = n 1 → . n 2 → n 1 → . n 2 → = 13 65
Đáp án cần chọn là B
Dùng phương pháp tọa độ hóa.
Đặt hệ trục tọa độ, ở đây như thầy đã trình bày ta nên chọn gốc tại P trục Ox, Oy là PA và PC.
Gọi α góc tạo bởi hai mặt phẳng ( AB'C' ) và (MNP)
Khi đó cos α = n 1 → . n 2 → n 1 → . n 2 → = 13 65
Đáp án cần chọn là B
Cho hình lăng trụ tam giác đều ABC.A'B'C' có A B = 2 3 và AA'=2. Gọi M, N, P lần lượt là trung điểm của các cạnh A'B', A'C' và BC. Côsin của góc tạo bởi hai mặt phẳng (AB'C') và (MNP) bằng:
A. 6 13 65
B. 13 65
C. 17 13 65
D. 18 63 65
Cho hình lăng trụ tam giác đều A B C . A ' B ' C ' có A B = 2 3 và AA' = 2 Gọi M, N, P lần lượt là trung điểm của các cạnh A'B', A'C' và BC. Côsin của góc tạo bởi hai mặt phẳng (AB'C') và (MNP) bằng:
A. 6 13 65 .
B. 13 65 .
C. 17 13 65 .
D. 18 63 65 .
Cho hình lăng trụ tam giác đều A B C . A ' B ' C ' có A B = 2 3 và A A ' = 2 . Gọi M và N lần lượt là trung điểm của A ' C ' và A ' B ' . Tính cosin của góc tạo bởi hai mặt phẳng A B ' C ' và (BCMN).
A. 13 65
B. - 13 65
C. 13 130
D. - 13 130
Cho hình lăng trụ tam giác đều ABC A'B'C' có A B = 2 3 và A A ' = 2 . Gọi M và N lần lượt là trung điểm của A'C' và A'B'. Tính cosin của góc tạo bởi hai mặt phẳng A B ' C ' và B C M N .
A. 13 65
B. − 13 65
C. 13 130
D. − 13 130
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có A B = 2 3 và AA’=2. Gọi M,N,P lần lượt là trung điểm của các cạnh A’B’, A’C’ và BC. Côsin của góc tạo bởi hai mặt phẳng (AB’C’) và (MNP) bằng
A. 6 13 65
B. 13 65 .
C. 17 13 65 .
D. 18 63 65 .
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có tất cả các cạnh bằng a. Gọi M,N lần lượt là trung điểm các cạnh AB,B′C′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng MN và AC bằng
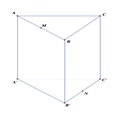
A. 1 3
B. 5 3
C. 2 3
D. 5 5
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có tất cả các cạnh bằng a. Gọi M,N lần lượt là trung điểm các cạnh AB,B′C′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng MN và AC bằng
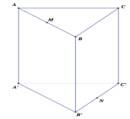
A. 1 3 .
B. 5 3 .
C. 2 3 .
D. 5 5 .
Cho khối lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại A, AB=a, BC=2a, A'B vuông góc với mặt phẳng (ABC) và góc giữa A'C và mặt phẳng (ABC) bằng 30 0 (tham khảo hình vẽ bên). Tính thể tích khối lăng trụ
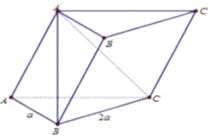
A. a 3 3
B. 3 a 3
C. a 3
D. a 3 6
Cho hình lăng trụ tam giác A B C . A ' B ' C ' có đáy là tam giác ABC vuông tại A, A B = 3 , A C = 4 và A A ' = 61 2 . Hình chiếu của B’ lên mặt phẳng A B C là trung điểm cạnh BC, điểm M là trung điểm cạnh A ' B ' . Tính cosin của góc tạo bởi hai mặt phẳng A M C ' và (A’BC) bằng:
A. 11 3157 .
B. 13 65 .
C. 33 3517 .
D. 33 3157 .