Các câu hỏi tương tự
Cho hình lăng trụ
A
B
C
.
A
B
C
Gọi E, F lần lượt là trung điểm của BB¢ và CC¢. Mặt phẳng
(
A
E
F
)
chia khối lăng trụ thành hai phần có thể tích
V
1
và
V
2
như hình vẽ. Tỉ số
V
1
V...
Đọc tiếp
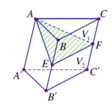
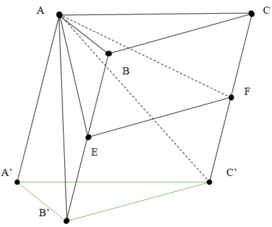
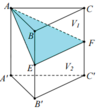
Cho hình lăng trụ A B C . A ' B ' C ' Gọi E, F lần lượt là trung điểm của BB¢ và CC¢. Mặt phẳng ( A E F ) chia khối lăng trụ thành hai phần có thể tích V 1 và V 2 như hình vẽ. Tỉ số V 1 V 2 là
A. 1 2
B. 1
C. 1 3
D. 1 4
Cho hình lăng trụ
A
B
C
.
A
B
C
. Gọi E, F lần lượt là trung điểm của BB và CC. Mặt phẳng
A
E
F
chia khối lăng trụ thành 2 phần có thể tích
V
1
và
V
2
như hình vẽ. Khi đó tỉ số
V
1...
Đọc tiếp
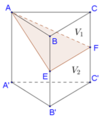
Cho hình lăng trụ A B C . A ' B ' C ' . Gọi E, F lần lượt là trung điểm của BB' và CC'. Mặt phẳng A E F chia khối lăng trụ thành 2 phần có thể tích V 1 và V 2 như hình vẽ. Khi đó tỉ số V 1 V 2 có giá trị là
A. 1 4
B. 1 2
C. 1 3
D. 3 4
Cho khối lăng trụ ABC.ABC . Gọi M là trung điểm của BB , N là điểm trên cạnh CC sao cho
C
N
N
C
. Mặt phẳng ( AMN ) chia khối lăng trụ thành hai phần có thể tích V1 và V2 như hình vẽ. Tính tỉ số
V
1
V
2
.
A.
V
1
V...
Đọc tiếp
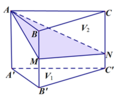
Cho khối lăng trụ ABC.A'B'C' . Gọi M là trung điểm của BB' , N là điểm trên cạnh CC' sao cho C N = N C ' . Mặt phẳng ( AMN ) chia khối lăng trụ thành hai phần có thể tích V1 và V2 như hình vẽ. Tính tỉ số V 1 V 2 .
A. V 1 V 2 = 5 3 .
B. V 1 V 2 = 3 2 .
C. V 1 V 2 = 4 3 .
D. V 1 V 2 = 7 5 .
Cho hình lăng trụ tam giác ABC.ABC. Gọi M,N lần lượt là trung điểm của BB,CC. Mặt phẳng (AMN) chia khối lăng trụ thành hai phần,
V
1
là thể tích của phần đa diện chứa điểm
B
,
V
2
thể tích phần đa diện còn lại. Tính tỉ số
V
1
V
2
A.
V
1
V
2...
Đọc tiếp
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M,N lần lượt là trung điểm của BB',CC'. Mặt phẳng (A'MN) chia khối lăng trụ thành hai phần, V 1 là thể tích của phần đa diện chứa điểm B , V 2 thể tích phần đa diện còn lại. Tính tỉ số V 1 V 2
A. V 1 V 2 = 7 2
B. V 1 V 2 = 2
C. V 1 V 2 = 3
D. V 1 V 2 = 5 2
Cho lăng trụ ABC.A’B’C’ có thể tích V, gọi M, N, P lần lượt thuộc cạnh AA’; BB’; CC’ sao cho
2
M
A
M
A
,
N
B
N
B
;
3
P
C
P
C
. Mặt phẳng chia khối lăng trụ
A
B
C
.
A
B
C...
Đọc tiếp
Cho lăng trụ ABC.A’B’C’ có thể tích V, gọi M, N, P lần lượt thuộc cạnh AA’; BB’; CC’ sao cho 2 M A = M A ' , N B = N B ' ; 3 P C = P C ' . Mặt phẳng chia khối lăng trụ A B C . A ' B ' C ' thành hai phần. Tính tỉ số thể tích hai phần này (số bé chia số lớn).
A. 17 19
B. 17 36
C. 13 23
D. 13 36
Cho khối lăng trụ tam giác
A
B
C
.
A
B
C
. Gọi M, N lần lượt là trung điểm của BB và CC. Mặt phẳng (AMN) chia khối lăng trụ thành hai khối đa diện. Gọi
V
1
là thể tích của khối đa thức diện chứa đỉnh B và
V
2
là thể tích khôi đa diện còn lại. Tính tỉ số
V
1...
Đọc tiếp
Cho khối lăng trụ tam giác A B C . A ' B ' C ' . Gọi M, N lần lượt là trung điểm của BB' và CC'. Mặt phẳng (A'MN) chia khối lăng trụ thành hai khối đa diện. Gọi V 1 là thể tích của khối đa thức diện chứa đỉnh B và V 2 là thể tích khôi đa diện còn lại. Tính tỉ số V 1 V 2
A. V 1 V 2 = 7 2
B. V 1 V 2 = 2
C. V 1 V 2 = 3
D. V 1 V 2 = 5 2
Cho lăng trụ tam giác ABC.A′B′C′. Gọi M,N,P lần lượt là trung điểm các cạnh A′B′,BC,CC′. Mặt phẳng (MNP) chia khối lăng trụ thành hai phần, phần chưa điểm B có thể tích là
V
1
.
Gọi V là thể tích khối lăng trụ. Tính
V
1
V
. A.
25
288
B.
29
144
C.
37...
Đọc tiếp
Cho lăng trụ tam giác ABC.A′B′C′. Gọi M,N,P lần lượt là trung điểm các cạnh A′B′,BC,CC′. Mặt phẳng (MNP) chia khối lăng trụ thành hai phần, phần chưa điểm B có thể tích là V 1 . Gọi V là thể tích khối lăng trụ. Tính V 1 V .
A. 25 288
B. 29 144
C. 37 288
D. 19 144
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của BB’, CC’. Mặt phẳng (A’MN) chia khối lăng trụ thành hai phần,
V
1
là thể tích của phần đa diện chứa điểm B,
V
2
là phần đa diện còn lại. Tính tỉ số
V
1
V
2
A.
V
1...
Đọc tiếp
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của BB’, CC’. Mặt phẳng (A’MN) chia khối lăng trụ thành hai phần, V 1 là thể tích của phần đa diện chứa điểm B, V 2 là phần đa diện còn lại. Tính tỉ số V 1 V 2
A. V 1 V 2 = 7 2
B. V 1 V 2 = 2
C. V 1 V 2 = 3
D. V 1 V 2 = 5 2
Cho hình lăng trụ ABC.ABC có thể tích bằng V. Gọi M, N lần lượt là trung điểm của AB, AC và P là điểm thuộc cạnh CC sao cho CP2CP (như hình vẽ). Tính thể tích khối tứ diện BMNP theo V A.
V
3
B.
2
V
9
C.
4
V
9
D.
5...
Đọc tiếp
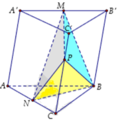
Cho hình lăng trụ ABC.A'B'C' có thể tích bằng V. Gọi M, N lần lượt là trung điểm của A'B', AC và P là điểm thuộc cạnh CC' sao cho CP=2C'P (như hình vẽ). Tính thể tích khối tứ diện BMNP theo V
A. V 3
B. 2 V 9
C. 4 V 9
D. 5 V 24